a:

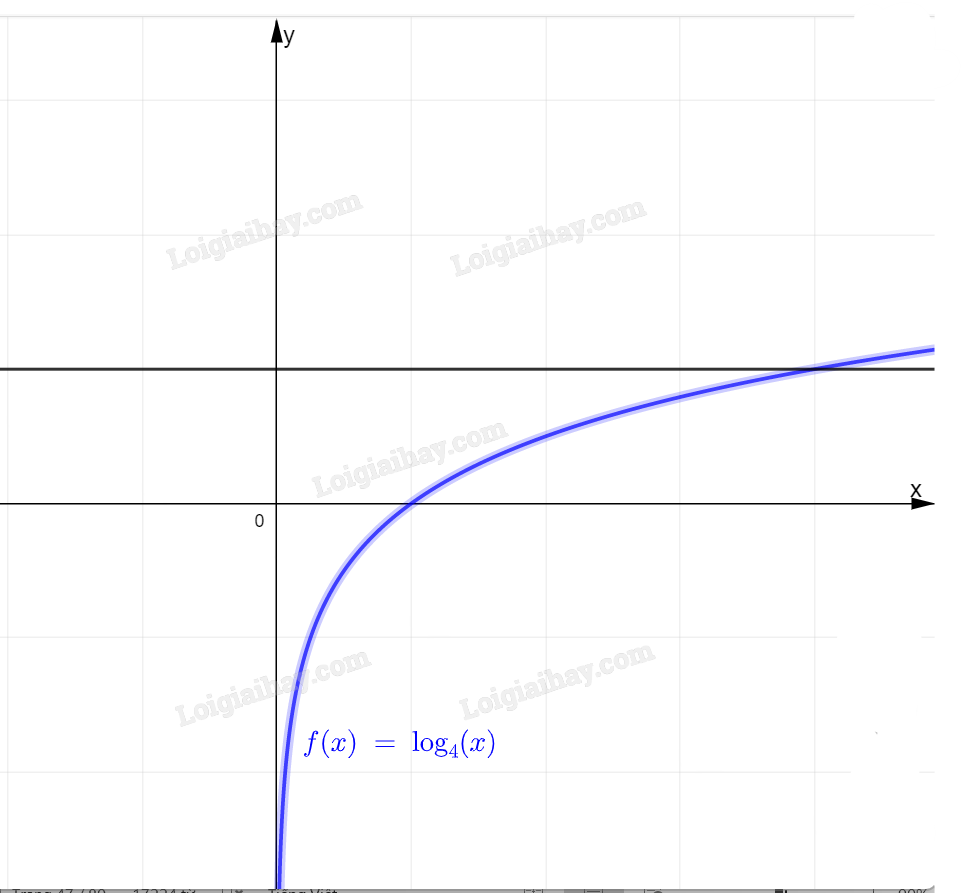
b: Hai đồ thị này có 1 giao điểm

=>Phương trình \(log_4x=5\) có 1 nghiệm duy nhất

a)     Do hoành độ giao điểm nằm trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) nên:  \(\tan x = m \Leftrightarrow \tan x = \tan \alpha  \Leftrightarrow x = \alpha  + k\pi \)

b)     Nhận xét: trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\), với mọi \(m \in \mathbb{R}\) ta luôn có \(x = \alpha  + k\pi \)

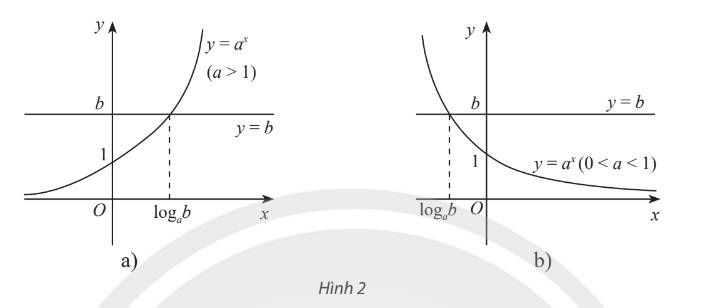
Khi \(b > 0\), đồ thị của hai hàm số \(y = {a^x}\) và \(y = b\) cắt nhau tại một điểm duy nhất. Khi đó phương trình \({a^x} = b\) có nghiệm duy nhất \(x = {\log _a}b\).

Khi \(b \le 0\), đồ thị của hai hàm số \(y = {a^x}\) và \(y = b\) không có điểm chung. Khi đó phương trình \({a^x} = b\)  vô nghiệm.

tham khảo.

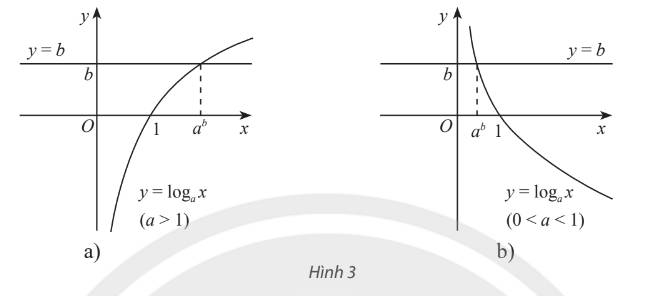
Đồ thị của hai hàm số \(y=\log_ax\) và \(y=b\) luôn cắt nhau tại một điểm duy nhất. Khi đó phương trình \(\log_ax=b\)  có nghiệm duy nhất \(x=a^b\).

a) Đồ thị hàm số (hình bên).

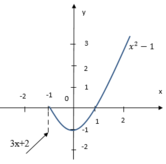
Quan sát đồ thị nhận thấy :

+ f(x) liên tục trên các khoảng (-∞ ; -1) và (-1 ; ∞).

+ f(x) không liên tục tại x = -1.

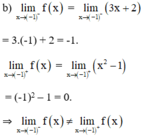
⇒ không tồn tại giới hạn của f(x) tại x = -1.

⇒ Hàm số không liên tục tại x = -1.

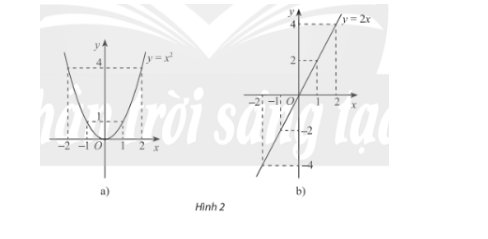
* Hàm số \(y = {x^2}\)

Nhìn đồ thị ta thấy:

+ \(y(1) = y( - 1) = 1,y(2) = y( - 2) = 4\)

+ Đồ thị hàm số đối xứng qua trục Oy.

* Hàm số \(y = 2x\)

Nhìn đồ thị ta thấy:

+ \(y(1) =  - y( - 1),y(2) =  - y( - 2)\)

+ Đồ thị hàm số đối xứng qua điểm O.

- Giả sử Δx là số gia của đối số tại xo = 1. Ta có:

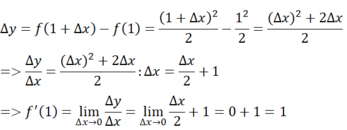
- Đường thẳng có hệ số góc bằng f'(1) = 1 có dạng:

y = 1.x + a hay y = x + a

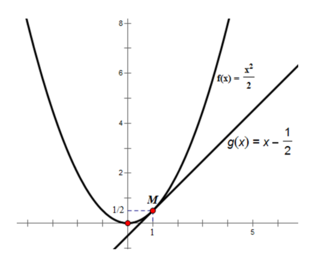
Mà đường thẳng đó đi qua điểm M(1;1/2) nên có: 1/2 = 1 + a ⇒ a = 1/2 - 1 = -1/2

⇒ đường thẳng đi qua M và có hệ số góc bằng 1 là: y = x – 1/2

Ta có đồ thị như trên. Đường thẳng y = x – 1/2 tiếp xúc với đồ thị hàm số f(x) tại M

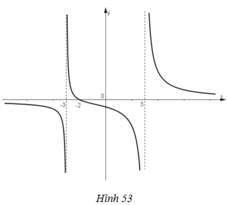
a) Quan sát đồ thị nhận thấy:

f(x) → 0 khi x → -∞

f(x) → -∞ khi x → 3-

f(x) → +∞ khi x → (-3)+.

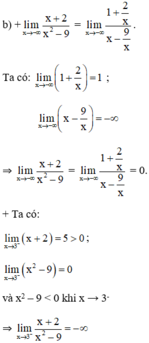
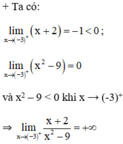
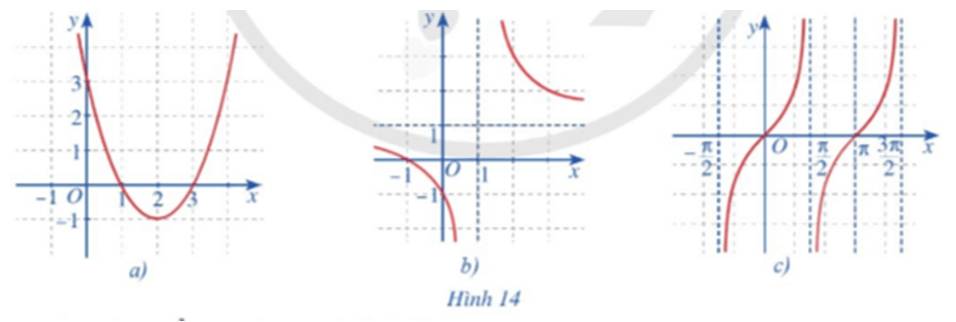
Hình 14a đồ thị là đường cong Parabol liền mạch nên hàm số liên tục trên toàn bộ trên khoảng xác định.

Hình 14b đồ thị bị chia làm hai nhánh:

- Với x < 1 ta thấy hàm số là một đường cong liền nên liên tục.

- Với x > 1 ta thấy hàm số là một đường cong liền nên liên tục.

Vậy hàm số liên tục trên từng khoảng xác định.

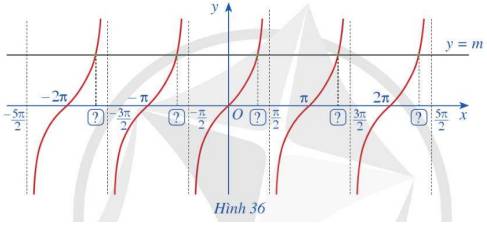
Hình 14c đồ thị hàm số y = tanx chia thành nhiều nhánh, và mỗi nhánh là các đường cong liền. Do đó hàm số liên tục trên mỗi khoảng xác định của chúng.