Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b) Ta có: \(x^2y+xy+x+1\)
\(=xy\left(x+1\right)+\left(x+1\right)\)
\(=\left(x+1\right)\left(xy+1\right)\)
c) Ta có: \(ax+by+ay+bx\)
\(=a\left(x+y\right)+b\left(x+y\right)\)
\(=\left(x+y\right)\left(a+b\right)\)

a, `(8x^3-4x^2): 4x -(4x^2-5x) : 2x + (2x)^2`
`=4x (2x^2-x) : 4x - 2x(2x-5/2 ) :2x + 4x^2`
`=2x^2-x-2x+5/2+4x^2`
`=6x^2-3x+5/2`
b, `(3x^3-x^2y) :x^2 -(xy^2+x^2y) :xy + 2x(x+1)`
`=x^2 (3x-y) :x^2 -xy(y+x) + (2x^2+2x)`
`=3x-y-y-x+2x^2+2x`
`=2x^2+4x-2y`

a) x2y+xy+x+1= (x2y+xy)+(x+1)=xy(x+10+(x+1)=(x+1)(xy+1)
b) x2-(a+b)x+ab=x2-ax-bx+ab=(x2-ax)-(bx-ab)=x(x-a)-b(x-a)=(x-a)(x-b)
c) ax2+ay-bx2-by=(ax2+ay)-(bx2+by)=a(x2+y)-b(x2+y)=(a-b)(x2+y)
d) ax-2x-a2+2a=(ax-2x)-(a2-2a)=x(a-2)-a(a-2)=(a-2)(x-a)
e) 2x2+4ax+x+2a=(2x2+4ax)+(x+2a)=2x(x+2a)+(x+2a)=(x+2a)(2x+1)
f) x3+ax2+x+a=(x3+ax2)+(x+a)=x2(x+a)+(x+a)=(x2+1)(x+a)

a. 3xy( 4x + y - \(\dfrac{4}{3}\) )
b. 2x2( 3x + 1 )
c. (2x + 3 )( x - y )
d. xy( 1 - x )( x - 1 )
e. 6( 2x + 1 )( x + y )

\(1,\\ a,A=4x^2\left(-3x^2+1\right)+6x^2\left(2x^2-1\right)+x^2\\ A=-12x^4+4x^2+12x^2-6x^2+x^2=-x^2=-\left(-1\right)^2=-1\\ b,B=x^2\left(-2y^3-2y^2+1\right)-2y^2\left(x^2y+x^2\right)\\ B=-2x^2y^3-2x^2y^2+x^2-2x^2y^3-2x^2y^2\\ B=-4x^2y^3-4x^2y^2+x^2\\ B=-4\left(0,5\right)^2\left(-\dfrac{1}{2}\right)^3-4\left(0,5\right)^2\left(-\dfrac{1}{2}\right)^2+\left(0,5\right)^2\\ B=\dfrac{1}{8}-\dfrac{1}{4}+\dfrac{1}{4}=\dfrac{1}{8}\)
\(2,\\ a,\Leftrightarrow10x-16-12x+15=12x-16+11\\ \Leftrightarrow-14x=-4\\ \Leftrightarrow x=\dfrac{2}{7}\\ b,\Leftrightarrow12x^2-4x^3+3x^3-12x^2=8\\ \Leftrightarrow-x^3=8=-2^3\\ \Leftrightarrow x=2\\ c,\Leftrightarrow4x^2\left(4x-2\right)-x^3+8x^2=15\\ \Leftrightarrow16x^3-8x^2-x^3+8x^2=15\\ \Leftrightarrow15x^3=15\\ \Leftrightarrow x^3=1\Leftrightarrow x=1\)

\(a,=\dfrac{\left(x+1\right)\left(x+y\right)}{\left(x-y\right)\left(x+1\right)}=\dfrac{x+y}{x-y}\\ b,=\dfrac{\left(x-3\right)^2}{3x\left(x-3\right)}=\dfrac{x-3}{3x}\\ c,=\dfrac{\left(y-x\right)\left(y+x\right)}{xy\left(x-y\right)}=\dfrac{-x-y}{xy}\)
Lời giải:
a.
\(\frac{x^2+xy+x+y}{x^2-xy+x-y}=\frac{x(x+y)+(x+y)}{x(x+1)-y(x+1)}=\frac{(x+y)(x+1)}{(x+1)(x-y)}=\frac{x+y}{x-y}\)
b.
\(\frac{x^2-6x+9}{3x^2-9x}=\frac{(x-3)^2}{3x(x-3)}=\frac{x-3}{3x}\)
c.
\(\frac{y^2-x^2}{x^2y-xy^2}=\frac{(y-x)(y+x)}{-xy(y-x)}=\frac{x+y}{-xy}\)
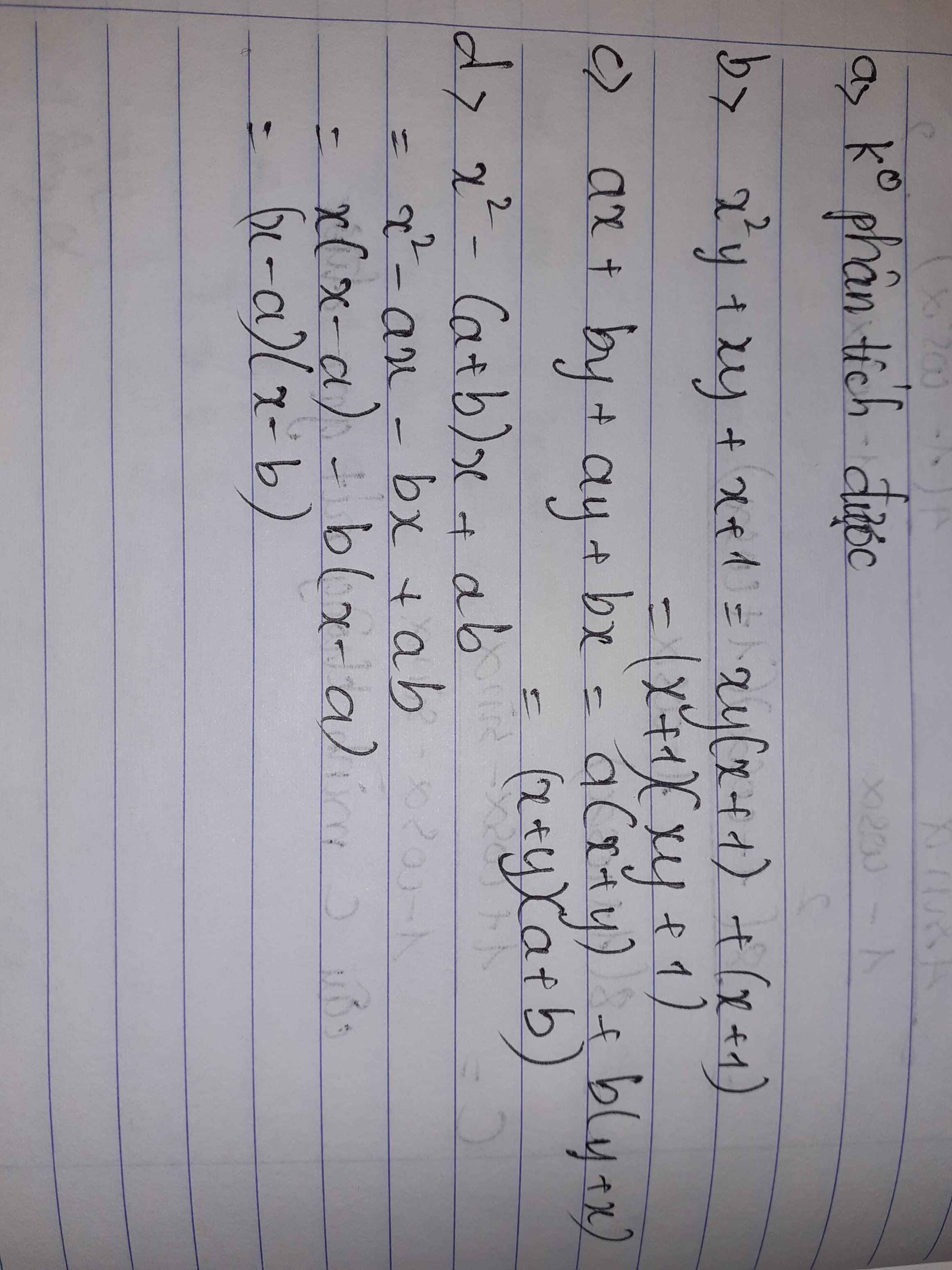
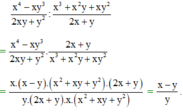
a) Ta có:\(A=\frac{x^2y+xy}{x^2y-y}=\frac{xy\left(x+1\right)}{y\left(x^2-1\right)}=\frac{x+1}{\left(x+1\right)\left(x+1\right)}=\frac{1}{x-1}\)
\(B=\frac{-2x^2}{x^3-x}=\frac{-2x^2}{x\left(x^2-1\right)}=\frac{-2x}{\left(x+1\right)\left(x-1\right)}\)
b) \(A+B=\frac{1}{x-1}+\frac{-2x}{\left(x+1\right)\left(x-1\right)}=\frac{x+1}{\left(x-1\right)\left(x+1\right)}+\frac{-2x}{\left(x-1\right)\left(x+1\right)}\)
\(=\frac{x+1-2x}{\left(x+1\right)\left(x-1\right)}=\frac{-\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}=-\frac{1}{x+1}\)