
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


6) \(\left(2x+\dfrac{1}{2}\right)^3=8x^3+4x^2+\dfrac{3}{2}x+\dfrac{1}{8}\)
7) \(\left(x-3\right)^3=x^3-9x^2+27x-27\)

Bài 1:
a: =3x(x+2)
b: \(=x\left(x-1\right)^2\)
c: \(=x^2\left(x-y\right)-\left(x-y\right)=\left(x-y\right)\left(x-1\right)\left(x+1\right)\)


b)\(3x\left(x+3y\right)-6xy\left(x+3y\right)\)
\(=\left(3x-6xy\right)\left(x+3y\right)\)
c)\(x\left(x+y\right)-5x-5y\)
\(=x\left(x+y\right)-5\left(x+y\right)\)
\(=\left(x-5\right)\left(x+y\right)\)
Bài 1:
b. \(3x\left(x+3y\right)-6xy\left(x+3y\right)\)
= (3x - 6xy)(x + 3y)
= 3x(1 - 2y)(x + 3y)
c. \(x\left(x+y\right)-5x-5y\)
= x(x + y) - 5(x + y)
= (x - 5)(x + y)
d. \(3\left(x-y\right)-5x\left(y-x\right)\)
= 3(x - y) + 5x(x - y)
= (3 + 5x)(x - y)
Bài 3:
a. x + 6x2 = 0
<=> x(1 + 6x) = 0
<=> \(\left[{}\begin{matrix}x=0\\1+6x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{-1}{6}\end{matrix}\right.\)
b. 2(x + 3) - x(x + 3) = 0
<=> (2 - x)(x + 3) = 0
<=> \(\left[{}\begin{matrix}2-x=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-3\end{matrix}\right.\)
c. 5x(x - 2) - (2 - x) = 0
<=> 5x(x - 2) + (x - 2) = 0
<=> (5x + 1)(x - 2) = 0
<=> \(\left[{}\begin{matrix}5x+1=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-1}{5}\\x=2\end{matrix}\right.\)
d. (x + 1) = (x + 1)2
<=> (x + 1) - (x + 1)2 = 0
<=> (1 - x - 1)(x + 1) = 0
<=> -x(x + 1) = 0
<=> \(\left[{}\begin{matrix}-x=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)



(3-12x)(x-1)+(12x-8)(x+2)+x2=52
3(x-1)-12x(x-1)+12x(x+2)-8(x+2)+x2=52
3x-3-12x2+12+12x2+24x-8x-16+x2=52
(3x+24x-8x)+(12-3-16)+(12x2-12x2+x2)=52
19x-7+x2=52
x(19-x)=52+7=59
mà 59 là số ng tố nên x rỗng
Vậy x E \(\theta\)

Bài 2:
Ta có: \(3n^3+10n^2-5⋮3n+1\)
\(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow3n\in\left\{0;-3;3\right\}\)
hay \(n\in\left\{0;-1;1\right\}\)

11)11) 3x(x-5)2-(x+2)3+2(x-1)3-(2x+1)(4x2-2x+1)=3x(x2-10x+25)-(x3+6x2+12x+8)+2(x3-3x2+3x-1)-(8x3+1)=3x3-30x2+75x-x3-6x2-12x-8+2x3-6x2+6x-2-8x3-1=-4x3-42x2+63x-11
 ai giúp em với ạ :3 e cảm ơn m.ng trước !! thân ái
ai giúp em với ạ :3 e cảm ơn m.ng trước !! thân ái
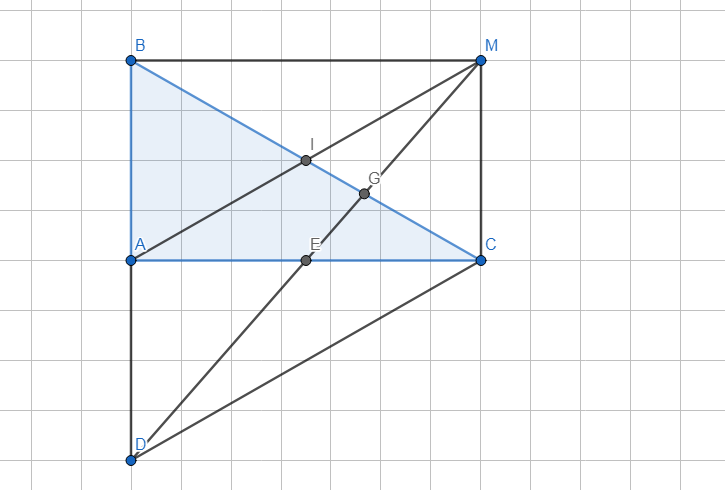
 ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn
ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn


