$\frac{x}{\sqrt{x+2}}+\sqrt{x+1}=\sqrt{3x+1}$$\frac{x}{\sqrt{x+2}}+\sqrt{x+1}=\sqrt{3x+1}$

a: ta có: ΔOBC cân tại O

mà OA là đường cao

nên OA là phân giác của góc BOC

Xét ΔOBA và ΔOCA có

OB=OC

\(\widehat{BOA}=\widehat{COA}\)

OA chung

Do đó: ΔOBA=ΔOCA

=>\(\widehat{OBA}=\widehat{OCA}=90^0\)

=>AC là tiếp tuyến của (O)

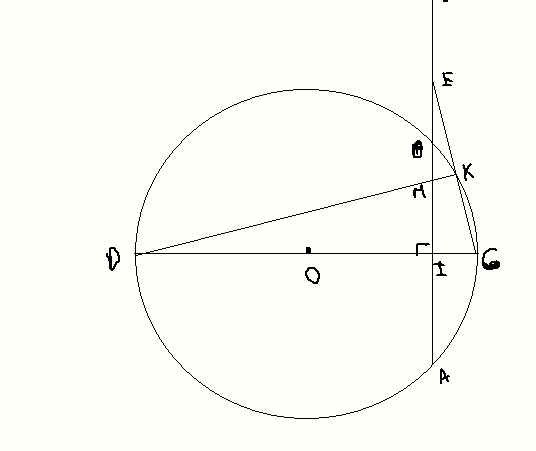
b: Ta có: OA//BD

BC\(\perp\)OA

Do đó: BD\(\perp\)BC

=>ΔBDC vuông tại B

Ta có: ΔBDC vuông tại B

=>ΔBDC nội tiếp đường tròn đường kính CD

mà ΔBDC nội tiếp (O)

nên CD là đường kính của (O)

c: Xét (O) có

ΔDEC nội tiếp

DC là đường kính

Do đó: ΔDEC vuông tại E

=>EC\(\perp\)ED tại E

=>CE\(\perp\)AD tại E

Xét ΔCDA vuông tại C có CE là đường cao

nên \(AE\cdot AD=AC^2\left(1\right)\)

Xét ΔCOA vuông tại C có CH là đường cao

nên \(AH\cdot AO=AC^2\left(2\right)\)

Từ (1) và (2) suy ra \(AE\cdot AD=AH\cdot AO\)

=>\(\dfrac{AE}{AO}=\dfrac{AH}{AD}\)

Xét ΔAEH và ΔAOD có

\(\dfrac{AE}{AO}=\dfrac{AH}{AD}\)

\(\widehat{EAH}\) chung

Do đó: ΔAEH đồng dạng vớiΔAOD

=>\(\widehat{AEH}=\widehat{AOD}\)

mà \(\widehat{AEH}+\widehat{DEH}=180^0\)(hai góc kề bù)

nên \(\widehat{DEH}+\widehat{AOD}=180^0\)

=>\(\widehat{DEH}+\widehat{DOH}=180^0\)

=>DEHO là tứ giác nội tiếp

=>\(\widehat{ODH}=\widehat{OEH}\)

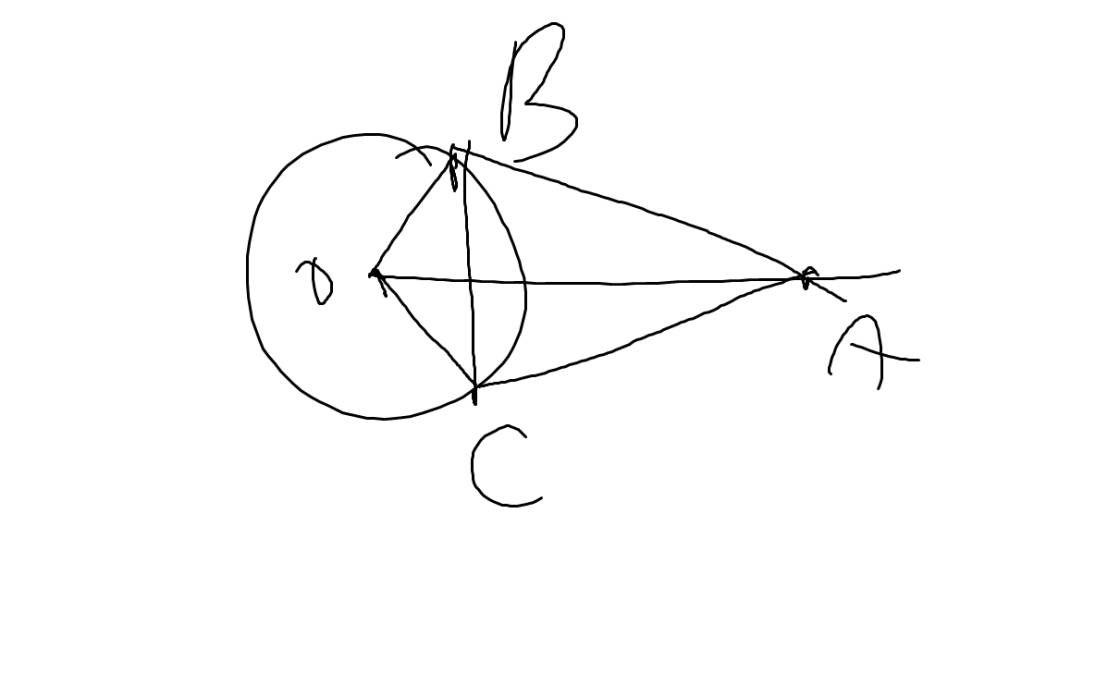
a: AB và AC là hai tiếp tuyến cắt nhau tại A

b: Xét tứ giác OBAC có

\(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)

=>OBAC là tứ giác nội tiếp

=>O,B,A,C cùng thuộc 1 đường tròn

a: Xét (O) có

ΔAMB nội tiếp

AB là đường kính

Do đó: ΔAMB vuông tại M

=>\(\widehat{AMB}=90^0\)

b: Xét ΔOMC vuông tại M có MH là đường cao

nên \(HC\cdot HO=HM^2\left(1\right)\)

Xét ΔMAB vuông tại M có MH là đường cao

nên \(HA\cdot HB=HM^2\left(2\right)\)

Từ (1) và (2) suy ra \(HC\cdot HO=HA\cdot HB\)

c: Xét tứ giác AMBQ có

O là trung điểm của AB và MQ

Do đó: AMBQ là hình bình hành

Hình bình hành AMBQ có AB=MQ

nên AMBQ là hình bình hành

nếu mik bt lm thì đâu cần thì mik đăng làm j

vcl