10: Ta có: \(\left(\dfrac{x+1}{x}\right)^2:\left[\dfrac{x^2+1}{x^2}+\dfrac{2}{x+1}\cdot\left(\dfrac{1}{x+1}+1\right)\right]\)

\(=\dfrac{\left(x+1\right)^2}{x^2}:\left(\dfrac{x^2+1}{x^2}+\dfrac{2\cdot\left(x+2\right)}{\left(x+1\right)^2}\right)\)

\(=\dfrac{\left(x+1\right)^2}{x^2}:\dfrac{\left(x^2+1\right)\left(x^2+2x+1\right)+2x^2\left(x+2\right)}{x^2\left(x+1\right)^2}\)

\(=\dfrac{\left(x+1\right)^2}{x^2}\cdot\dfrac{x^2\left(x+1\right)^2}{x^4+2x^3+x^2+x^2+2x+1+2x^3+4x^2}\)

\(=\dfrac{\left(x+1\right)^4}{x^4+4x^3+6x^2+2x+1}\)

cho quãng đường ko z

pro minecraft and miniworld Huhu ko có :(((

Bài 1: 

a: =3x(x+2)

b: \(=x\left(x-1\right)^2\)

c: \(=x^2\left(x-y\right)-\left(x-y\right)=\left(x-y\right)\left(x-1\right)\left(x+1\right)\)

\(P=\left(x-y\right)^2+\left(x+y\right)^2-2\left(x-y\right)\left(x+y\right)-4x^2\\ P=\left(x-y-x-y\right)^2-4x^2\\ P=4y^2-4x^2=4\left(y-x\right)\left(x+y\right)\)

6) \(\left(2x+\dfrac{1}{2}\right)^3=8x^3+4x^2+\dfrac{3}{2}x+\dfrac{1}{8}\)

7) \(\left(x-3\right)^3=x^3-9x^2+27x-27\)

7: \(\left(x-3\right)^3=x^3-9x^2+27x-27\)

a.

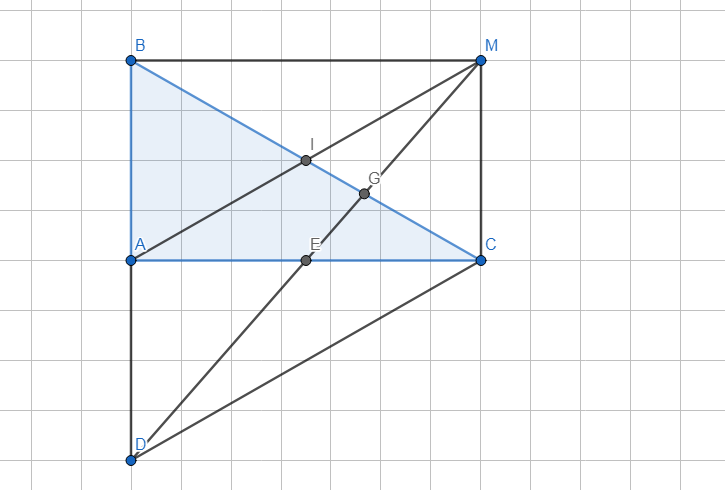
Ta có \(BD||AC\) (cùng vuông góc AB)

Áp dụng định lý Talet trong tam giác ACE: \(\dfrac{BE}{BA}=\dfrac{DE}{DC}\)

b.

Ta có \(IK||BD||AC\) \(\Rightarrow EI||AC\)

Áp dụng Talet: \(\dfrac{DC}{ED}=\dfrac{DA}{ID}\Rightarrow\dfrac{DC}{DC+ED}=\dfrac{DA}{DA+ID}\Rightarrow\dfrac{DC}{CE}=\dfrac{DA}{AI}\) (1)

Do \(BD||EK\), áp dụng Talet trong tam giác CEK: \(\dfrac{BD}{EK}=\dfrac{CD}{CE}\) (2)

Do \(BD||EI\), áp dụng Talet trong tam giác AEI: \(\dfrac{BD}{EI}=\dfrac{AD}{AI}\) (3)

Từ(1);(2);(3) \(\Rightarrow\dfrac{BD}{EK}=\dfrac{BD}{EI}\Rightarrow EK=EI\)

Chọn C

C nha bạn (hằng đẳng thức số 3)

HmJeDXk5ybc\XBWv...10-27.jpg k cho minh nha k dung e

Cả phần http://  ... bên trên nữa bạn, bạn copy hết nhé