
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2:
Ta có: \(3n^3+10n^2-5⋮3n+1\)
\(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow3n\in\left\{0;-3;3\right\}\)
hay \(n\in\left\{0;-1;1\right\}\)

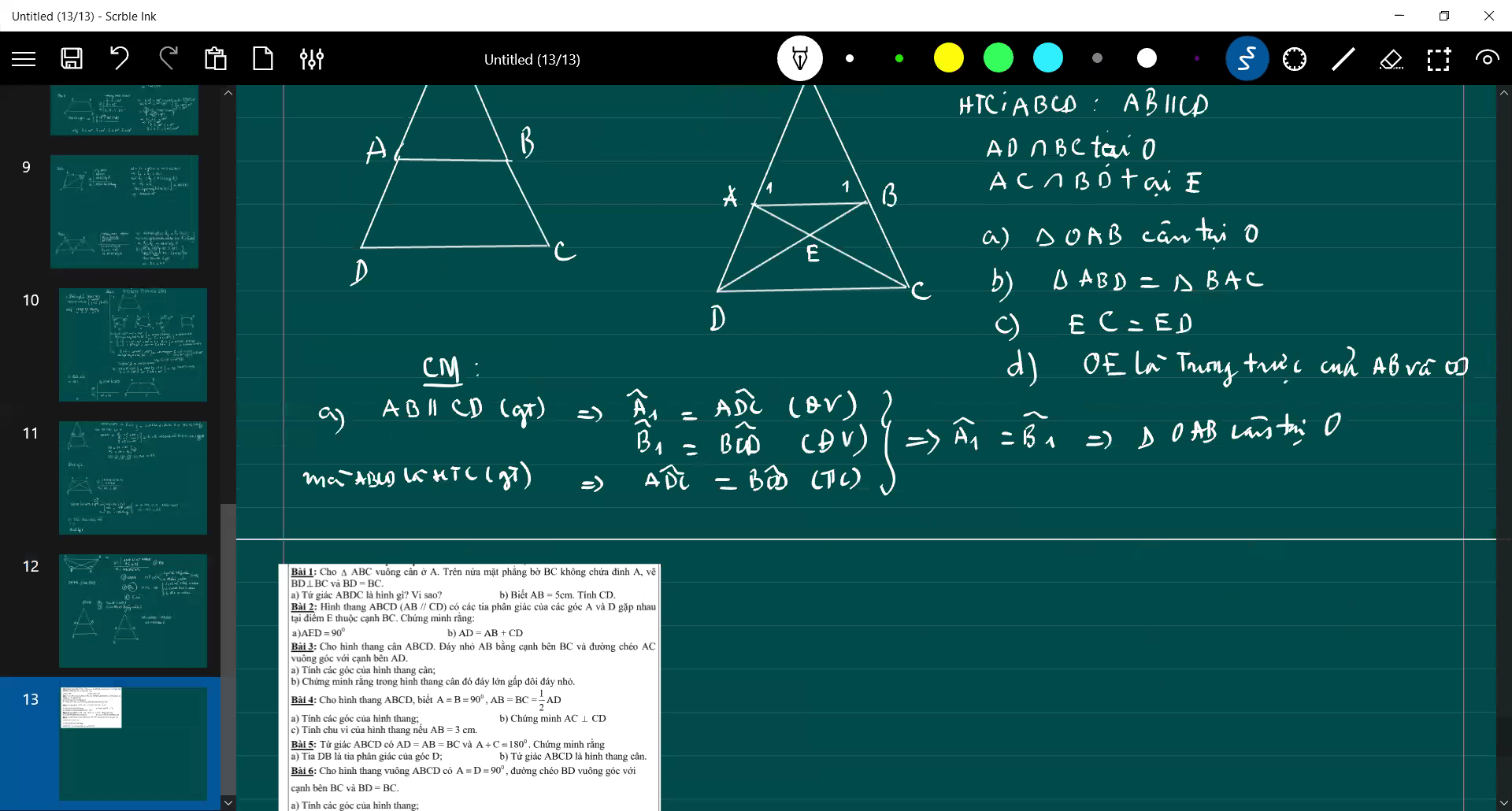
b: Xét ΔABD và ΔBAC có
BA chung
BD=AC
AD=BC
Do đó: ΔABD=ΔBAC
c: ta có: EA+EC=AC
EB+ED=BD
mà AC=BD
và EA=EB
nên EC=ED

c: Gọi bốn số nguyên liên tiếp là x;x+1;x+2;x+3
Ta có: \(x\left(x+1\right)\left(x+2\right)\left(x+3\right)+1\)
\(=\left(x^2+3x\right)\left(x^2+3x+2\right)+1\)
\(=\left(x^2+3x\right)^2+2\left(x^2+3x\right)+1\)
\(=\left(x^2+3x+1\right)^2\)
\(d,M=\left(x^2-4xy+4y^2\right)-2\left(x-2y\right)+1+9\\ M=\left(x-2y\right)^2-2\left(x-2y\right)+1+9\\ M=\left(x-2y+1\right)^2+9\ge9\\ M_{min}=9\Leftrightarrow x=2y-1\)

\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$

\(A=x^6-2x^4-2x^4+4x^2+2x^3-4x\\ A=x^3\left(x^3-2x\right)-2x\left(x^3-2x\right)+2\left(x^3-2x\right)\\ A=\left(x^3-2x\right)\left(x^3-2x+2\right)=3\left(3+2\right)=3\cdot5=15\\ B=x^5-2x^3+3x^3-6x-3x^2\\ =x^2\left(x^3-2x\right)+3\left(x^3-2x\right)-3x^2\\ =\left(x^3-2x\right)\left(x^2+3\right)-3x^2=3\left(x^2+3\right)-3x^2\\ =3x^2-3x^2+9=9\)

8) \(\dfrac{x+7}{3}+\dfrac{x+5}{4}=\dfrac{x+3}{5}+\dfrac{x+1}{6}\)
\(\Rightarrow\dfrac{x+7}{3}+\dfrac{x+5}{4}-\dfrac{x+3}{5}-\dfrac{x+1}{6}=0\)
\(\Rightarrow\dfrac{x+7}{3}+2+\dfrac{x+5}{4}+2-\dfrac{x+3}{5}-2-\dfrac{x+1}{6}-2=0+2+2-2-2\)
\(\Rightarrow\left(\dfrac{x+7}{3}+2\right)+\left(\dfrac{x+5}{4}+2\right)-\left(\dfrac{x+3}{5}+2\right)-\left(\dfrac{x+1}{6}+2\right)=0\)
\(\Rightarrow\left(\dfrac{x+7}{3}+\dfrac{6}{3}\right)+\left(\dfrac{x+5}{4}+\dfrac{8}{4}\right)-\left(\dfrac{x+3}{5}+\dfrac{10}{5}\right)-\left(\dfrac{x+1}{6}+\dfrac{12}{2}\right)=0\)
\(\Rightarrow\left(x+13\right)\left(\dfrac{1}{3}+\dfrac{1}{4}-\dfrac{1}{5}-\dfrac{1}{6}\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+13=0\\\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}=0\end{matrix}\right.\)
\(x+13=0\)
\(\Rightarrow x=-13\)
\(\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}=0\)
\(\dfrac{13}{60}=0\) (vô lí)
Vậy \(x=-13\)
9) Bạn chuyển vế rồi cộng 3 vào từng mỗi số

Bài 3:
\(a,=3x\left(y-4x+6y^2\right)\\ b,=5xy\left(x^2-6x+9\right)=5xy\left(x-3\right)^2\\ d,=\left(x+y\right)\left(x-12\right)\\ f,=2x\left(x-y\right)\left(5x-4y\right)\\ g,=\left(x-2\right)\left(x-2+3x\right)=\left(x-2\right)\left(4x-2\right)=2\left(x-2\right)\left(2x-1\right)\\ h,=x^2\left(1-5x\right)+3xy\left(5x-1\right)=x\left(1-5x\right)\left(x-3y\right)\\ i,=x\left(x-2\right)+4\left(x-2\right)=\left(x+4\right)\left(x-2\right)\\ j,=x^2-2x-3x+6=\left(x-2\right)\left(x-3\right)\\ k,=4x^2-12x+3x-9=\left(x-3\right)\left(4x+3\right)\\ l,=\left(x+5\right)^2-y^2=\left(x-y+5\right)\left(x+y+5\right)\\ m,=x^2-\left(2y-6\right)^2=\left(x-2y+6\right)\left(x+2y-6\right)\\ n,=\left(x^2+5x+4\right)\left(x^2+5x+6\right)-24\\ =\left(x^2+5x+5\right)^2-1-24\\ =\left(x^2+5x+5\right)^2-25\\ =\left(x^2+5x\right)\left(x^2+5x+10\right)\\ =x\left(x+5\right)\left(x^2+5x+10\right)\)
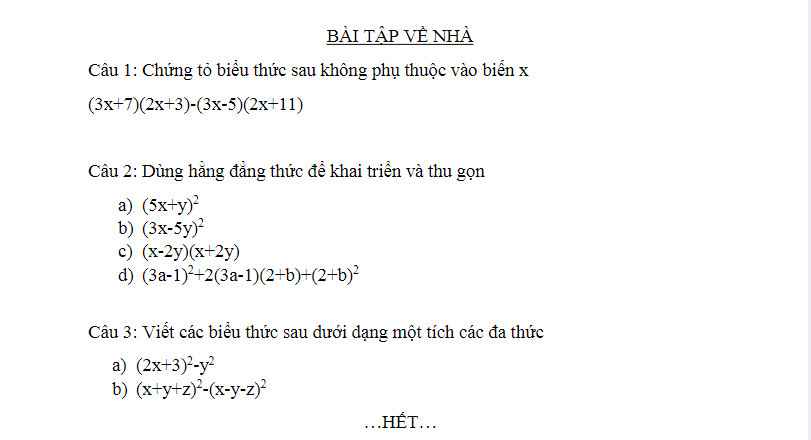





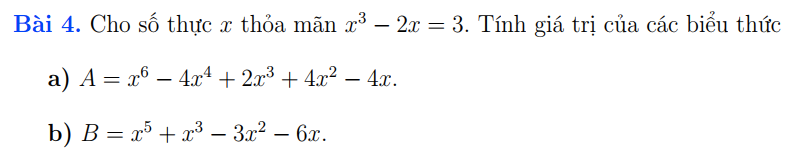


Câu 1:
Ta có: \(\left(3x+7\right)\left(2x+3\right)-\left(3x-5\right)\left(2x+11\right)\)
\(=6x^2+9x+14x+21-\left(6x^2+33x-10x-55\right)\)
\(=6x^2+23x+21-6x^2-23x+55\)
=76
cám ơn ạ