
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`sin3x sinx+sin(x-π/3) cos (x-π/6)=0`
`<=> 1/2 (cos2x - cos4x) + 1/2(-sin π/6 + sin (2x-π/2)=0`
`<=> cos2x-cos4x-1/2+ sin(2x-π/2)=0`
`<=>cos2x-cos4x-1/2+ sin2x .cos π/2 - cos2x. sinπ/2=0`
`<=> cos2x - cos4x - cos2x = 1/2`
`<=> cos4x = cos(2π)/3`
`<=>` \(\left[{}\begin{matrix}4x=\dfrac{2\text{π}}{3}+k2\text{π}\\4x=\dfrac{-2\text{π}}{3}+k2\text{π}\end{matrix}\right.\)
`<=>` \(\left[{}\begin{matrix}x=\dfrac{\text{π}}{6}+k\dfrac{\text{π}}{2}\\x=-\dfrac{\text{π}}{6}+k\dfrac{\text{π}}{2}\end{matrix}\right.\)





\(a,\Rightarrow x1,x2\in D=R\left(x1\ne x2\right)\)
\(\Rightarrow I=\dfrac{f\left(x1\right)-f\left(x2\right)}{x1-x2}=\dfrac{x1\left(m^2+1\right)+2m+1-x2\left(m^2+1\right)-2m-1}{x1-x2}\)
\(\Rightarrow I=\dfrac{\left(x1-x2\right)\left(m^2+1\right)}{x1-x2}=\dfrac{ }{ }\)\(m^2+1>0\Rightarrow I>0\Rightarrow\)\(hàm\) \(đb\left(D=R\right)\)
\(b,\Rightarrow x1,x2\in D=R\left(x1\ne x2\right)\)
\(\Rightarrow I=\dfrac{f\left(x1\right)-f\left(x2\right)}{x1-x2}=\dfrac{\left(m^2+1\right)\left(x1-x2\right)}{x1-x2}=m^2+1>0\Rightarrowđb\left(D=R\right)\)

1:
ĐKXĐ: \(-x^2+4x-2>=0\)
=>\(x^2-4x+2< =0\)
=>\(\left(x-2\right)^2-2< =0\)
=>\(-\sqrt{2}< =x-2< =\sqrt{2}\)
=>\(-\sqrt{2}+2< =x< =\sqrt{2}+2\)
\(\sqrt{-x^2+4x-2}=2-x\)
=>\(\left\{{}\begin{matrix}-x^2+4x-2=\left(2-x\right)^2\\2-x>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-x^2+4x-2=x^2-4x+4\\x< =2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-2x^2+8x-6=0\\2-\sqrt{2}< =x< =2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x^2-4x+3=0\\2-\sqrt{2}< =x< =2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(x-1\right)\left(x-3\right)=0\\2-\sqrt{2}< =x< =2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\in\left\{1;3\right\}\\2-\sqrt{2}< =x< =2\end{matrix}\right.\)
=>x=1
2: Bạn xem lại đề giúp mình nha, sao lại có 2 dấu bằng?

Gọi O là trọng tâm tam giác ABC.
Dựng hình bình hành ABCE.
Ta có \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MO}\).
\(\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{BA}+\overrightarrow{MC}=\overrightarrow{CE}+\overrightarrow{MC}=\overrightarrow{ME}\).
Từ đó \(T=3MO+3ME\ge3OE\).
Dấu bằng xảy ra khi và chỉ khi M là giao của OE và AC, tức M là trung điểm của AC.
Vậy...



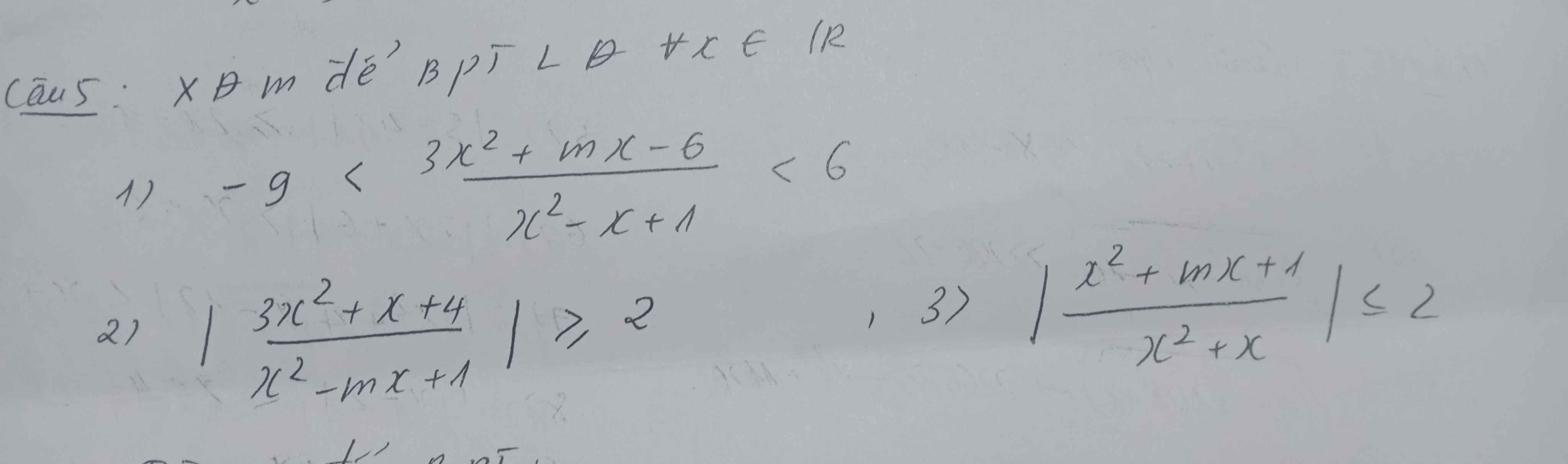






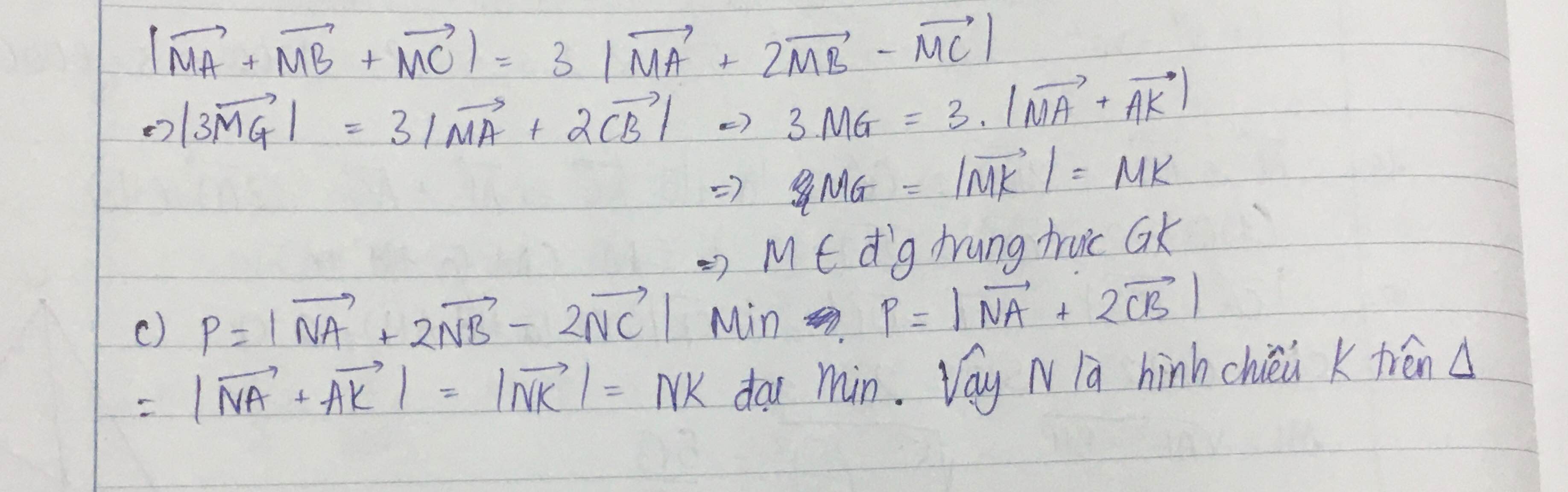 Từ câu a suy ra đc vecto AK = 2 lần vecto CB nhé.
Từ câu a suy ra đc vecto AK = 2 lần vecto CB nhé.
1: \(\overrightarrow{AG}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)