
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Vì ME là tiếp tuyến đường tròn O và M là tiếp điểm
=> \(MO\perp MF\) ( t/c tiếp tuyến ) hay ^OME = 900
Vậy tam giác EMO là tam giác vuông tại M
b, mình sửa đề là OE = 60 cm nhé
Theo định lí Pytago cho tam giác EMO vuông tại M
\(ME=\sqrt{EO^2-OM^2}=48\)cm
c, sửa ON vuông OE tại N
đến đây thì mình chả hiểu đề kiểu gì, chịu, bạn chép đề kiểu gì ấy, sai tào lao sao á, xem lại nhé
a: Xét ΔMEO có \(\widehat{OME}=90^0\)
nên ΔMEO vuông tại M

Câu 5:
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
c: Xét tứ giác AEDF có
\(\widehat{EAF}=\widehat{AFD}=\widehat{AED}=90^0\)
Do đó: AEDF là hình chữ nhật
mà AD là tia phân giác của \(\widehat{FAE}\)
nên AEDF là hình vuông


1: mx-y=3 và 3x+my=5
=>y=mx-3 và 3x+m(mx-3)=5
=>x(m^2+3)=3m+5 và y=mx-3
=>x=(3m+5)/(m^2+3) và \(y=\dfrac{3m^2+5m-3m^2-9}{m^2+3}=\dfrac{5m-9}{m^2+3}\)
2x+y<m+21/m^2+3
=>6m+10+5m-9<m+21
=>11m+1<m+21
=>m<2
2:
Gọi số chi tiết đội 1 và đội 2 sản xuất được trong tháng đầu lần lượt là a,b
Theo đề, ta có hệ:
a+b=900 và 1,1a+1,15b=1015
=>a=400 và b=500

\(\sqrt{a^2+3}=\sqrt{a^2+ab+bc+ca}=\sqrt{\left(a+b\right)\left(a+c\right)}\le\dfrac{1}{2}\left(a+b+a+c\right)=\dfrac{1}{2}\left(2a+b+c\right)\)
Tương tự: \(\sqrt{b^2+3}\le\dfrac{1}{2}\left(a+2b+c\right)\) ; \(\sqrt{c^2+3}\le\dfrac{1}{2}\left(a+b+2c\right)\)
Cộng vế với vế:
\(VT\le\dfrac{1}{2}\left(4a+4b+4c\right)=2\left(a+b+c\right)\)

\(=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}-1}+\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}+1}\)
\(=\sqrt{x}+\sqrt{x}=2\sqrt{x}\)

1.theo bất đẳng thức côsi ta có
\(a+b\ge2\sqrt{ab}\\ b+c\ge2\sqrt{ab}\\ c+a\ge2\sqrt{ab}\)
\(\Rightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge8\sqrt{ab.bc.ca}\)
\(\ge8\sqrt{a^2b^2c^2}\\ \ge8abc\)
2.\(a^4+b^2\ge2\sqrt{a^4b^2}=2a^4b^2\)
\(\dfrac{a}{a^4+b^2}\le\dfrac{a}{2a^2b}=\dfrac{1}{2ab}\)
tương tự:\(\dfrac{b}{b^4+a^2}\le\dfrac{1}{2ab}\)
\(\rightarrow\dfrac{a}{a^4+b^2}+\dfrac{b}{b^4+a^2}\le\dfrac{1}{ab}\)
dấu = xảy ra khi \(a^4=b^2\\ b^4=a^2\)\(\rightarrow a^2=b^2=1\)

bạn tự vẽ hình giúp mik nha
a. xét \(\Delta ADN\) và \(\Delta BAM\) có
AB=AD(gt)
\(\widehat{ADN}=\widehat{BAM}=90^o\)
DN=MA(N,M là trung điểm của cạnh DC,AD)
\(\Rightarrow\Delta ADN\sim\Delta BAM\left(c.g.c\right)\)
\(\Rightarrow\widehat{DNA}=\widehat{AMB}\)
mà:\(\widehat{DNA}+\widehat{DAN}=90^o\Rightarrow\widehat{BMA}+\widehat{DAN}=90^o\)
\(\Rightarrow\Delta MAI\) vuông tại I
\(\Rightarrow AI\perp MI\) hay \(MB\perp AN\)
b.ta có M là trung điểm của AD\(\Rightarrow AM=\dfrac{1}{2}AD=\sqrt{5}\)
trong \(\Delta MAB\) vuông tại A có
\(MB=\sqrt{AM^2+AB^2}=\sqrt{\sqrt{5^2}+\left(2\sqrt{5}\right)^2}=5\)
\(AM^2=MB.MI\Rightarrow MI=\dfrac{AM^2}{MB}=\dfrac{\sqrt{5^2}}{5^5}=0,2\)
\(AI.MB=AM.AB\Rightarrow AI=\dfrac{AM.AB}{MB}=\dfrac{\sqrt{5}.2\sqrt{5}}{5}\)=2
c.IB=MB-MI=5-0,2=4,8
\(S_{\Delta AIB}=\dfrac{AI.IB}{2}=\)\(\dfrac{2.4,8}{2}=4,8\)
\(S_{\Delta ADN}=\dfrac{AD.DN}{2}=\dfrac{2\sqrt{5}.\sqrt{5}}{2}=5\)
\(S_{\Delta ABCD}=\left(2\sqrt{5}\right)^2=20\)
\(S_{BINC}=S_{ABCD}-S_{\Delta AIB}-S_{\Delta DAN}\)=20-4,8-5=10,2

Bài 3:
1: ĐKXĐ: \(x\ge1\)
2: ĐKXĐ: \(x\in R\)
3: ĐKXĐ: \(x\le1\)
4: ĐKXĐ: \(x>\dfrac{3}{2}\)





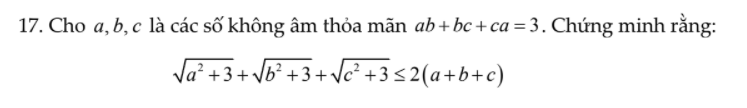 câu này với ạ! Mình cảm ơn.
câu này với ạ! Mình cảm ơn.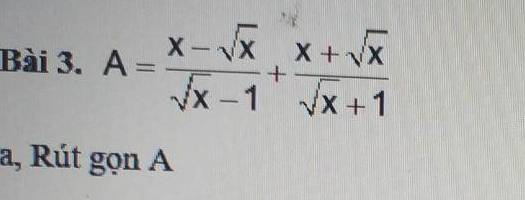
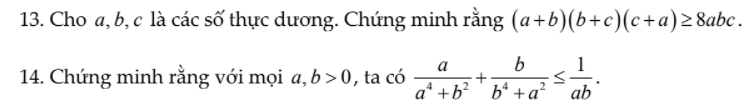



c) Ta có: \(\sqrt{\sqrt{x}+3}=3\)
\(\Leftrightarrow\sqrt{x}+3=9\)
\(\Leftrightarrow\sqrt{x}=6\)
hay x=36
Ta có: \(\sqrt{x-2\sqrt{x-1}}=2\)
\(\Leftrightarrow x-2\sqrt{x-1}-4=0\)
\(\Leftrightarrow x-1-2\cdot\sqrt{x-1}\cdot1+1=4\)
\(\Leftrightarrow\left(\sqrt{x-1}-1\right)^2=4\)
\(\Leftrightarrow\sqrt{x-1}-1=2\)
\(\Leftrightarrow\sqrt{x-1}=3\)
\(\Leftrightarrow x-1=9\)
hay x=10