
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



51)
| 4 | 9 | 2 |
| 3 | 5 | 7 |
| 8 | 1 | 6 |
52)a) 14 . 15 = (14 : 2) . ( 50 . 2) 16 . 25 = (16: 4 ) . ( 25 . 4)
= 7 . 100 = 4 . 100
= 700 = 400

( x + 15 ) - 97 = 215
x + 15 = 215 + 97
x + 15 = 312
x = 312 - 15
x = 297
A
<=>x+15=215+97=312
<=>x =312-15
<=>x =297
B
<=>2x=238-84=154
<=>x =154:2
<=>x =77
C
<=>x-93=7
<=>x =7+93
<=>x =100

P=2.4.6.8.16.32.64.128.256.512.1024.2^52
=2^1.2^2.2^3. .... .2^10.2^52
=2^(1+2+3+...+10+52)=2^107

11: \(27+12+\left(-17\right)+\left(-12\right)\)
\(=\left(27-17\right)+\left(12-12\right)\)
=10+0
=10
12: \(-564-\left(324-564-224\right)\)
\(=-564-\left(-564+100\right)\)
\(=-564+564-100=-100\)
13: \(2^3\cdot3^2-7^2-2022^0\)
\(=8\cdot9-49-1\)
=72-50
=22
14: \(236\cdot145+236\cdot856-236\)
\(=236\cdot145+236\cdot856-236\cdot1\)
\(=236\left(145+856-1\right)\)
\(=236\cdot1000=236000\)
15: \(-\left(-357\right)+27+\left(-357\right)+\left(-32\right)\)
\(=357+27-357-32\)
=27-32
=-5
16: \(275\cdot48+22\cdot275+175\left(-70\right)\)
\(=275\left(48+22\right)-175\cdot70\)
\(=275\cdot70-175\cdot70\)
\(=70\left(275-175\right)=70\cdot100=7000\)
17: \(\dfrac{\left(23\cdot36-17\cdot36\right)}{36}\)
\(=\dfrac{36\left(23-17\right)}{36}\)
=23-17
=6
18: \(3\cdot5^3-27:3^2+5^3\cdot4-18:3^2\)
\(=3\cdot5^3+4\cdot5^3-27:9-18:9\)
\(=5^3\left(3+4\right)-3-2\)
\(=125\cdot7-5=875-5=870\)
19: \(-87+\left(-12\right)-\left(-487\right)+512\)
\(=-87-12+487+512\)
\(=\left(487-87\right)+\left(512-12\right)\)
=400+500
=900
20: \(25\cdot57+75+33\cdot25+75\cdot89\)
\(=25\cdot57+25\cdot33+75+75\cdot89\)
\(=25\left(57+33\right)+75\left(1+89\right)\)
\(=25\cdot100+100\cdot75\)
\(=100\left(25+75\right)=100\cdot100=10000\)

Lời giải:
Ta có:
$10\equiv -1\pmod {11}$
$\Rightarrow 10^{2022}\equiv (-1)^{2022}\equiv 1\pmod {11}$
$\Rightarrow A=10^{2022}-1\equiv 1-1\equiv 0\pmod {11}$
Vậy $A\vdots 11$
ok
A= 10^2022-1
Ta có thể thấy 10^2022=100000000...........0000000000
10000000.......0000000000-1 thì lúc nnày tổng bằng
9999999999999999........................999999999999999999999
mà 99999999999999999999999....................9999999999999999999chia hết cho 11 nên tổng này chia hết cho 11

x-1=3 hoặc x-1=-3
=>x=4 => x=-2
............................
học tốt!!!!!!!!!!!!!!
\(\left|x-1\right|=3\)
\(\Leftrightarrow\orbr{\begin{cases}x-1=3\\x-1=-3\end{cases}\Leftrightarrow\orbr{\begin{cases}x=4\\x=-2\end{cases}}}\)
Vậy x=4; x=-2


Giải:
a)\(\dfrac{3}{4}x-\dfrac{1}{3}=\dfrac{-5}{6}\)
\(\dfrac{3}{4}x=\dfrac{-5}{6}+\dfrac{1}{3}\)
\(\dfrac{3}{4}x=\dfrac{-1}{2}\)
\(x=\dfrac{-1}{2}:\dfrac{3}{4}\)
\(x=\dfrac{-2}{3}\)
b)\(\left(2\dfrac{4}{5}x-0,2\right):\dfrac{4}{5}=\dfrac{7}{8}\)
\(\dfrac{14}{5}x-\dfrac{1}{5}=\dfrac{7}{8}.\dfrac{4}{5}\)
\(\dfrac{14}{5}x-\dfrac{1}{5}=\dfrac{7}{10}\)
\(\dfrac{14}{5}x=\dfrac{7}{10}+\dfrac{1}{5}\)
\(\dfrac{14}{5}x=\dfrac{9}{10}\)
\(x=\dfrac{9}{10}:\dfrac{14}{5}\)
\(x=\dfrac{9}{28}\)
c) \(\dfrac{1}{4}+\dfrac{1}{3}:\left|2x-1\right|=\dfrac{11}{12}\)
\(\dfrac{1}{3}:\left|2x-1\right|=\dfrac{11}{12}-\dfrac{1}{4}\)
\(\dfrac{1}{3}:\left|2x-1\right|=\dfrac{2}{3}\)
\(\left|2x-1\right|=\dfrac{1}{3}:\dfrac{2}{3}\)
\(\left|2x-1\right|=\dfrac{1}{2}\)
⇒2x-1=\(\dfrac{1}{2}\) hoặc 2x-1=\(\dfrac{-1}{2}\)
x=\(\dfrac{3}{4}\) hoặc x=\(\dfrac{1}{4}\)
câu a nha \(\dfrac{3}{4}x-\dfrac{1}{3}=-\dfrac{5}{6}\)
\(\dfrac{3}{4}x=-\dfrac{5}{6}+\dfrac{1}{3}\)
\(\dfrac{3}{4}x=-\dfrac{3}{6}\)
\(x=-\dfrac{3}{6}:\dfrac{3}{4}\)
\(x=-\dfrac{6}{4}.\dfrac{4}{3}\)
\(x=-\dfrac{24}{12}=-2\)


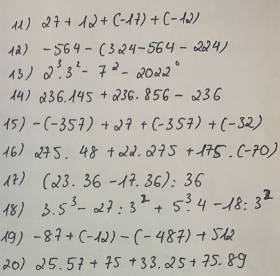 giúp mình với ai nhanh mình tick cho
giúp mình với ai nhanh mình tick cho

Bài 15:
a. Với $x$ nguyên, để $A=\frac{x+5}{x-2}$ nguyên thì:
$x+5\vdots x-2$
$\Rightarrow x-2+7\vdots x-2$
$\Rightarrow 7\vdots x-2$
$\Rightarrow x-2\in \left\{\pm 1; \pm 7\right\}$
$\Rightarrow x\in \left\{3; 1; 9; -5\right\}$
b.
Với $x$ nguyên, để $A=\frac{2x-3}{x+1}$ nguyên thì:
$2x-3\vdots x+1$
$\Rightarrow 2(x+1)-5\vdots x+1$
$\Rightarrow 5\vdots x+1$
$\Rightarrow x+1\in \left\{\pm 1; \pm 5\right\}$
$\Rightarrow x\in \left\{0; -2; 4; -6\right\}$
Bài 16:
a.
\(2009.\frac{2009^{2008}+1}{2009^{2009}+1}=\frac{2009^{2009}+2009}{2009^{2009}+1}=1+\frac{2008}{2009^{2009}+1}< 1+\frac{2008}{2009^{2008}+1}=\frac{2009^{2008}+2009}{2009^{2008}+1}=2009.\frac{2009^{2007}+1}{2009^{2008}+1}\)
\(\Rightarrow \frac{2009^{2008}+1}{2009^{2009}+1}< \frac{2009^{2007}+1}{2009^{2008}+1}\)
b.
\(\frac{7^{58}+2}{7^{57}+2}=\frac{7(7^{57}+2)-12}{7^{57}+2}=7-\frac{12}{7^{57}+2}\)
\(\frac{7^{57}+2009}{7^{56}+2009}=\frac{7(7^{56}+2009)-12054}{7^{56}+2009}=7-\frac{12054}{7^{56}+2009}\)
Ta thấy:
\(\frac{12}{7^{57}+2}=\frac{6}{\frac{7^{57}}{2}+1}<\frac{6}{\frac{7^{56}}{2009}+1}= \frac{12054}{7^{56}+2009}\)
\(\Rightarrow 7-\frac{12}{7^{57}+2}> 7-\frac{12054}{7^{56}+2009}\Rightarrow \frac{7^{58}+2}{7^{57}+2}>\frac{7^{57}+2009}{7^{56}+2009}\)