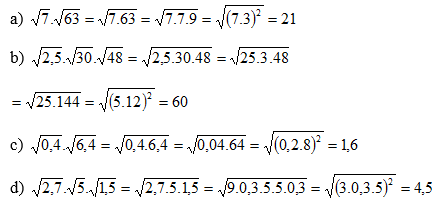a)\(\sqrt{10}\cdot\sqrt{40}=\sqrt{10\cdot40}=\sqrt{400}=20\)

b) \(\sqrt{2}\cdot\sqrt{162}=\sqrt{2\cdot162}=\sqrt{2\cdot2\cdot81}=\sqrt{4}\cdot\sqrt{81}=2\cdot9=18\)

a) \(\sqrt{10}.\sqrt{40}\)

=\(\sqrt{10.40}\)

=\(\sqrt{400}\)

=20

b) \(\sqrt{5.}\sqrt{45}\)

=\(\sqrt{5.45}\)

=\(\sqrt{225}\)

=\(\sqrt{15}\)

c) \(\sqrt{52.}\sqrt{13}\)

=\(\sqrt{52.13}\)

=\(\sqrt{676}\)

=26

d)\(\sqrt{2.}\sqrt{162}\)

=\(\sqrt{2.162}\)

=\(\sqrt{324}\)

=18

b)

=15

Áp dụng quy tắc chia hai căn bậc hai, hãy tính :

a) 2300−−−−√23−−√ = \(\sqrt{\dfrac{2300}{23}}\) = \(\sqrt{100}\) = 10

b) 12,5−−−−√0,5−−−√ = \(\sqrt{\dfrac{12,5}{0,5}}\) = \(\sqrt{25}\) = 5

c) 192−−−√12−−√ = \(\sqrt{\dfrac{192}{12}}\) = \(\sqrt{16}\) = 4

d) 6–√150−−−√ = \(\sqrt{\dfrac{6}{150}}\) = \(\sqrt{\dfrac{1}{25}}\) = \(\dfrac{1}{5}\)

a) = \(\sqrt{10.40}=\sqrt{400}=\sqrt{20^2}=20\)

b) \(=\sqrt{5.45}=\sqrt{5^2.3^2}=\sqrt{15^2}=15\)

a) \(\sqrt{0,4}.\sqrt{6,4}=\sqrt{0,4.6,4}=\sqrt{\frac{4}{10}.\frac{64}{10}}=\sqrt{\frac{\left(2.8\right)^2}{10^2}}=\frac{16}{10}=\frac{8}{5}\)

b) \(\sqrt{2,7}.\sqrt{5}.\sqrt{1,5}=\sqrt{\frac{27}{10}.5.\frac{15}{10}}=\sqrt{\frac{3^3.5^2.3}{10^2}}=\sqrt{\frac{\left(3^2.5\right)^2}{10^2}}=\frac{45}{10}=\frac{9}{2}\)

câu này dễ mà

chỉ cần nhân vào là xong

kiến thức đầu lớp 9 khá dễ đấy

tự mình làm đi nha bạn

Ta thấy các số trong căn bậc hai đều lớn hơn 0, áp dụng \(\sqrt{a\cdot b}=\sqrt{a}\cdot\sqrt{b}\)

a) \(\sqrt{7}\cdot\sqrt{63}=\sqrt{7\cdot63}=21\)

b) \(\sqrt{2,5}\cdot\sqrt{30}\cdot\sqrt{48}=\sqrt{2,5\cdot30\cdot48}=60\)

c) \(\sqrt{0,4}\cdot\sqrt{6,4}=\sqrt{0,4\cdot6,4}=1,6\)

d) \(\sqrt{2,7}\cdot\sqrt{5}\cdot\sqrt{1,5}=\sqrt{2,7\cdot5\cdot1,5}=4,5\)

a. \(\sqrt{7}.\sqrt{63}=\sqrt{7.63}=\sqrt{441}=21\)

b.\(\sqrt{2,5}.\sqrt{30}.\sqrt{48}=\sqrt{2,5.30.48}=\sqrt{3600}=60\)

c.\(\sqrt{0,4}.\sqrt{6,4}=\sqrt{0,4.6,4}=\sqrt{2,56}=1,6\)

d.\(\sqrt{2,7}.\sqrt{5}.\sqrt{1,5}=\sqrt{2,7.5.1,5}=\sqrt{20,25}=4,5\)

Học tốt nhé :)

a)\(\sqrt{7.63}\)=21

b)\(\sqrt{2,5.30.48}\)=60

c)\(\sqrt{0,4.6,4}\)=1,6

d)\(\sqrt{2,7.5.1,5}\)=4,5

Áp dụng quy tắc khai phương một tích

1: Ta có: \(\sqrt{\frac{1}{5}}\cdot\sqrt{\frac{1}{20}}\cdot3\cdot7\)

\(=\sqrt{\frac{1}{5}}\cdot\sqrt{\frac{1}{20}}\cdot\sqrt{9}\cdot\sqrt{49}\)

\(=\sqrt{\frac{1}{5}\cdot\frac{1}{20}\cdot9\cdot49}\)

\(=\sqrt{\frac{441}{100}}=\frac{\sqrt{441}}{\sqrt{100}}=\frac{21}{10}\)

2: Ta có: \(\sqrt{0,001\cdot360\cdot3^2\cdot\left(-3\right)^2}\)

\(=\sqrt{0,001}\cdot\sqrt{360}\cdot\sqrt{3^{^2}}\cdot\sqrt{\left(-3\right)^2}\)

\(=\sqrt{\frac{1}{100}}\cdot\sqrt{\frac{1}{10}}\cdot\sqrt{6^2}\cdot\sqrt{10}\cdot3\cdot3\)

\(=\frac{1}{10}\cdot6\cdot9\cdot\sqrt{\frac{1}{10}\cdot10}=\frac{54}{10}\cdot1=\frac{27}{5}\)

Áp dụng quy tắc nhân căn thức bậc hai

1: Ta có: \(2\sqrt{2}\left(4\sqrt{8}-\sqrt{32}\right)\)

\(=2\sqrt{2}\cdot4\sqrt{8}-2\sqrt{2}\cdot\sqrt{32}\)

\(=8\cdot\sqrt{16}-2\cdot\sqrt{64}\)

\(=8\cdot4-2\cdot8\)

=32-16=16

2300 23 = 2300 23 = 100 = 10