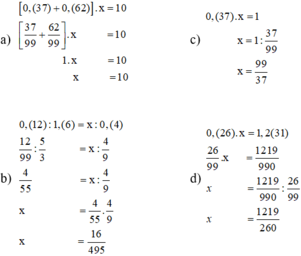minh ko biet

123x369+369x654-369x563+369+564789

=644124

K cho mk

Sửa: \(x^2+y^2=369\)

\(x:y=4:5\Rightarrow\dfrac{x}{4}=\dfrac{y}{5}\Rightarrow\dfrac{x^2}{16}=\dfrac{y^2}{25}=\dfrac{x^2+y^2}{16+25}=\dfrac{369}{41}=9\\ \Rightarrow\left\{{}\begin{matrix}x^2=144\\y^2=225\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\pm12\\y=\pm15\end{matrix}\right.\)

Vậy \(\left(x;y\right)=\left(12;15\right);\left(-12;-15\right)\)

Bài này khó quá =))

a) 0,(37)+0,(62) = 1

Có 0.(37)=\(\frac{37}{99}\)và  0.(62) = \(\frac{62}{99}\)

  \(\frac{37}{99}\)+     \(\frac{62}{99}\)= 1

\(\Rightarrow0,\left(37\right)+0.\left(62\right)=1\)

b)\(0,\left(37\right)\times3=1\)

Có: \(0,\left(37\right)=\frac{37}{99}\)

       \(\frac{37}{99}\times3=1\)

    \(\Rightarrow0\left(37\right)\times3=1\)

\(a,A=\left(x+2\right)^2+37\)

\(A_{min}=37\Leftrightarrow\left(x+2\right)^2=0\Rightarrow x+2=0\Leftrightarrow x=-2\)

\(b,B=2\left(x-3\right)^2-30\)

\(B_{min}=-30\Leftrightarrow2\left(x-3\right)^2=0\Rightarrow x-3=0\Leftrightarrow x=3\)

\(e,E=-\left(x+2\right)^2+37\)

\(E_{max}=37\Leftrightarrow-\left(x+2\right)^2=0\Rightarrow x+2=0\Leftrightarrow x=-2\)

a: \(\Leftrightarrow x\cdot\dfrac{3}{5}=\dfrac{-1}{7}+\dfrac{1}{2}=\dfrac{1}{2}-\dfrac{1}{7}=\dfrac{5}{14}\)

\(\Leftrightarrow x=\dfrac{5}{14}:\dfrac{3}{5}=\dfrac{25}{42}\)

b: =>|3x-1|=2

\(\Leftrightarrow\left[{}\begin{matrix}3x-1=2\\3x-1=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{3}\end{matrix}\right.\)

c: \(\Leftrightarrow7\left(37-x\right)=3\left(x-13\right)\)

=>259-7x=3x-39

=>-10x=-298

hay x=29,8

d: =>x=3/4+2/3=9/12+8/12=17/12

a) 0,4:x=x:0,9

0,4.0,9=x²

0,36 =x²

\(\sqrt{0,36}\)=x

0,6 =x

a) 0,4 : x = x : 0,9 x^2=0,9 . 0,4 x^2=(0,6)^2 =>x=+_6