Bài 1 . Cho tam giác ABC vuông tại A. Trên cạnh AC lấy các điểm M, N (M nằm giữa A, N). So sánh các độ dài BM, BN, BC.
Bài 2 Cho tam giác ABC, điểm M nằm giữa B và C. Gọi H và K là chân các đường vuông góc kẻ từ M đến các đường thẳng AB và AC. So sánh BC và tổng MH + MK.
Bài 3 Cho tam giác ABC có BC = 1 cm, AC = 7 cm. Tìm độ dài cạnh AB, biết độ dài này là một số nguyên (cm).
Bài 4 tam giác ABC, điểm M thuộc cạnh AB.
a) So sánh MC với AM + AC.
b) Chứng minh MB + MC < AB + AC.
- Cộng cùng một số vào hai vế của bất đẳng thức:
a< b => a + c < b + c.
- Cộng từng vế hai bất đẳng thức cùng chiều:
Bài 5 Cho tam giác ABC, điểm M bất kỳ nằm trong tam giác.
a) So sánh MB + MC với BC
b) Chứng minh MA + MB + MC >
Bài 6 Cho ABC có hai đường trung tuyến BD, CE
a) Tính các tỉ số
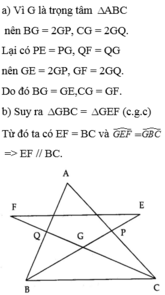
Bài 7 Cho tam giác ABC có hai đường trung tuyến BP, CQ cắt nhau tại G. Trên tia đối của tia PB lấy điểm E sao cho PE = PG. Trên tia đối của tia QG lấy điểm F sao cho QF = QG. Chứng minh:
a) GB = GE, GC = GE; b) EF = BC và EF//BC.
b) Chứng minh BD + CE > BC
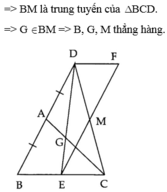
Bài 8 Cho ABC. Trên tia đối của tia AB lấy điểm D sao cho
AD = AB. Lấy G thuộc cạnh AC sao cho AG = AC. Tia DG cắt BC tại E. Qua E vẽ đường thẳng song song với BD, qua D vẽ đường thẳng song song với BC, hai đường thẳng này cắt nhau tại F. Gọi M là giao điểm của EF và CD.
Chứng minh:
a) G là trọng tâm BCD;
b) BED = FDE, từ đó suy ra EC = DF;
c) DMF = CME;
d) B, G, M thẳng hàng.
Bài 9. Cho ABC vuông tại A, AB = 6 cm, AC = 8 cm.
a) Tính BC.
b) Đường thẳng đi qua trung điểm I của BC và vuông góc với BC cắt AC tại D. Chứng minh .
c) Trên tia đối của tia DB lấy điểm E sao cho DE = DC. Chứng minh BCE vuông.
Bài 10 Cho tam giác ABC vuông tại A. Từ một điểm K bất kì trên cạnh BC, vẽ KH AC (HAC). Trên tia đối của tia HK lấy điểm I sao cho HI = HK. Chứng minh:
a) Chứng minh AB //HK;
b) Chứng minh
c) Chứng minh AKI cân,
Bài 11 Cho có tia phân giác Ot. Trên tia Ot lấy điểm C bất kì. Lấy
A Ox, B Oy sao cho OA = OB. Gọi H là giao điểm của AB và Ot. Chứng minh:
a) CA = CB và CO là phân giác của ;
b) OC vuông góc với AB tại trung điểm của AB;
c) Biết AB = 6 cm, OA = 5 cm. Tính OH


a:
Sửa đề: DE=DG
ta có: DE=DG
mà D nằm giữa G và E
nên D là trung điểm của GE
Ta có: QG=QF
mà Q nằm giữa F và G
nên Q là trung điểm của FG
Xét ΔABC có
BD,CQ là đường trung tuyến
BD cắt CQ tại G
Do đó: G là trọng tâm của ΔABC
=>BG=2GD; CG=2GQ
ta có: BG=2GD
mà GE=2GD
nên BG=GE
Ta có: CG=2GQ
mà GF=2GQ
nên CG=GF
b: Xét ΔGFE và ΔGCB có
GF=GC
\(\widehat{FGE}=\widehat{GCB}\)
GE=GB
Do đó: ΔGFE=ΔGCB
=>FE=CB
ta có: ΔGFE=ΔGCB
=>\(\widehat{GFE}=\widehat{GCB}\)
=>FE//BC