Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đổi 20 phút = \(\dfrac{1}{3}h\)
Gọi thời gian đi là: x (h) (x>0)
⇒ thời gian về là: \(x-\dfrac{1}{3}\) (h) (\(x>\dfrac{1}{3}\))
Theo bài ra, ta có pt:
\(30x=35\left(x-\dfrac{1}{3}\right)\)
\(35x-\dfrac{35}{3}=30x\)
\(5x=\dfrac{35}{3}\)
\(x=\dfrac{7}{3}\)\(\left(TM\right)\)
Quãng đường từ a đến b là:
\(30.\dfrac{7}{3}=70km\)
Vậy ...

Gọi quãng đường AB là x
=> Thời gian lúc đi là x/25
Thời gian lúc về là x/ 30
Vì thời gian về ít hơn thời gian đi là 20 phút = 1/3 h, nên ta có pt sau
x/25 - x/30 = 1/3
<=>6x/150 - 5x/ 150 = 50/ 150
<=> 6x - 5x = 50
<=> x= 50
Vậy quãng đường AB dài 50 km

$20'=\dfrac{1}{3}h$
Gọi $x(km)$ là độ dài quãng đường AB $(x>0)$
Thời gian đi từ A đến B là: $\dfrac{x}{40}(h)$
Vận tốc đi từ B về A là: $40+15=55(km/h)$
Thời gian đi từ B về A là: $\dfrac{x}{55}(h)$
Theo đề bài, ta có phương trình:
$\dfrac{x}{40}-\dfrac{x}{55}=\dfrac{1}{3}$
$⇔(\dfrac{1}{40}-\dfrac{1}{55}).x=\dfrac{1}{3}$
$⇔x=\dfrac{1}{3}:(\dfrac{1}{40}-\dfrac{1}{55})=\dfrac{440}{9}≃49 \ \ \text{(nhận)}$

gọi quãng đường AB là x (x>0)km
thời gian đi hết quãng đường AB là \(\dfrac{x}{30} h\)
quãng đường người đó đi lúc về dài 15+x km
thời gian về trên quãng đường đó \(\dfrac{15+x}{40}h\)
vì thời gian về ít hơn tg đi là 20p=\(\dfrac{1}{3}\)h nên ta có
\(\dfrac{x}{30}-\dfrac{15+x}{40}=\dfrac{1}{3}\)
giải pt x=85
vậy quãng đường AB dài 85 km
Gọi x (km) là quãng đường người đó đi về ( x>0)
Thời gian người đó đi từ A đến B : x : 30 = \(\dfrac{x}{30}\) (km/h)
Thời gian người đó đi về bằng con đường khác: x : 40 = \(\dfrac{x}{40}\) (km/h)
Vì lúc về người đó đi con đường khác về nên ít hơn thời gian đi là
20 phút (= \(\dfrac{1}{3}giờ\)) nên ta có phương trình
\(\dfrac{x}{30}-\dfrac{x}{40}=\dfrac{1}{3}\)
\(\dfrac{4x}{120}-\dfrac{3x}{120}=\dfrac{40}{120}\)
⇒ 4x -3x = 40
x= 40 ( km )
Quãng đường AB dài: 40 + 15 = 55 ( km )
Vậy quãng đường AB dài 55 km

45 phút = \(\dfrac{3}{4}h.\)
Gọi quãng đường AB là x (km) \(\left(x>0\right).\)
Thời gian đi từ A đến B là \(\dfrac{x}{48}\left(h\right).\)
Thời gian đi về là \(\dfrac{x}{48+12}=\dfrac{x}{60}\left(h\right).\)
Vì thời gian về ít hơn thời gian đi là 45 phút, nên ta có PT:
\(\dfrac{x}{60}+\dfrac{3}{4}=\dfrac{x}{48}.\\ \Rightarrow x=180\left(TM\right).\)

Gọi độ dài quãng đường AB là x (km), (x > 0, km)
Thời gian đi từ A đến B: 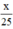 (giờ)
(giờ)
Thời gian đi từ B đến A: 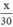 (giờ)
(giờ)
Thời gian về ít hơn thời gian đi 20 phút = 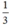 giờ nên ta có phương trình:
giờ nên ta có phương trình:
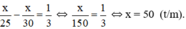
Vậy quãng đường AB dài 50km.
Bài 1.
Gọi số cần tìm là ab ( \(0< a\le9,0\le b\le9\))
Viết thêm chữ số 5 vào bên trái ta được số A
=> A = 5ab
Viết thêm chữ số 5 vào bên phải tâ được số B
=> B = ab5
Theo đề bài ta có : A - B = 153
<=> 5ab - ab5 = 153
<=> 500 + ab - ( ab.10 + 5 ) = 153
<=> 500 + ab - 10ab - 5 = 153
<=> 495 - 9ab = 153
<=> 9ab = 342
<=> ab = 38 ( tmđk )
Vậy số cần tìm là 38
Bài 2.
Gọi độ dài cạnh hình vuông đó là x ( m, x > 0 )
Tăng độ dài cạnh lên 12m => Độ dài mới = x + 12m
Diện tích ban đầu = x2 ( m2 )
Diện tích sau khi tăng = ( x + 12 )2 ( m2 )
Khi đó diện tích tăng 135m2
=> Ta có phương trình : x2 + 135 = ( x + 12 )2
<=> x2 + 135 = x2 + 24x + 144
<=> x2 - x2 - 24x = 144 - 135
<=> -24x = 9
<=> x = -9/24 = -3/8 ( Đến chỗ này nên xem lại đề )
Bài 3.
Gọi độ dài quãng đường AB là x ( km , x > 0 )
Thời gian người đó đi từ A đến B = x/25 ( giờ )
Thời gian người đó đi từ B về A = x/30 ( giờ )
Thời gian lúc về ít hơn thời gian lúc đi 20 phút = 1/3 giờ
=> Ta có phương trình : x/25 - x/30 = 1/3
<=> x( 1/25 - 1/30 ) = 1/3
<=> x . 1/150 = 1/3
<=> x = 50 ( tmđk )
Vậy quãng đường AB dài 50km