Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Xác suất để có đúng một máy hoạt động không tốt là 0 , 75. 1 − 0 , 85 + 1 − 0 , 75 0 , 85 = 0 , 325

Đáp án C.
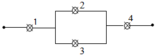
Để hoạt động tốt, mạch điện có thẻ có các trường hợp sau:
TH1: 1 tốt, 2 tốt,3 tốt, 4 tốt:
P 1 = 0 , 8.0 , 9.0 , 95.0.98 = 0 , 67032
TH2: 1 tốt, 2 tốt,3 cháy, 4 tốt:
P 1 = 0 , 8.0 , 9.0 , 05.0.98 = 0 , 03528
TH3: 1 tốt, 2 cháy,3 tốt, 4 tốt:
P 1 = 0 , 8.0 , 1.0 , 95.0.98 = 0 , 07448
Từ đó xác suất để mạch hoạt động tốt là:
0 , 67032 + 0 , 03528 + 0 , 07448 = 0 , 78008.

Từ giả thiết suy ra xác suất để người thứ nhất, thứ hai, thứ ba bắn không trúng đích lần lượt là 0,5; 0,4 và 0,2
Để có đúng người bắn trúng đích thì có các trường hợp sau
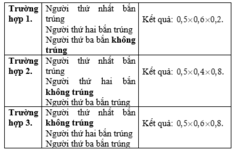
Vậy xác suất để có đúng người bắn trúng đích là
![]()
Chọn B.

Đáp án C
Gọi X ¯ là biến cố: Không một xạ thủ nào bắn trúng. Khi đó X ¯ = A ¯ ∪ B ¯ ∪ C ¯ . Do A, B, C độc lập với nhau nên A ¯ ; B ¯ ; C ¯ độc lập với nhau.
Suy ra P X ¯ = 0 , 3 . 0 , 4 . 0 , 5 = 0 , 06 ⇒ P X ¯ = 1 - P X ¯ = 0 , 94 .

Chọn A.
Phương pháp:
Áp dụng quy tắc cộng và nhân xác suất.
Cách giải:
Xác suất để có ít nhất một người bắn trúng là:
1 − 1 − 0 , 7 1 − 0 , 6 1 − 0 , 5 = 1 − 0 , 3.0 , 4.0 , 5 = 0 , 94

Chọn B.
Phương pháp
Tính xác suất theo phương pháp biến cố đối: “Không có cầu thủ nào sút vào”.
Cách giải:
Gọi A là biến cố: “Ít nhất một cầu thủ sút vào”.
Khi đó A ¯ là biến cố: “Không có cầu thủ nào sút vào”.


Chọn đáp án B.
Số bác sĩ tổng quát có hoạt động chuyên môn chính là giảng dạy bằng 258. Suy ra xác suất để chọn được một bác sĩ tổng quát có hoạt động chuyên môn chính là giảng dạy từ trong 607 bác sĩ phẫu thuật là 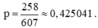


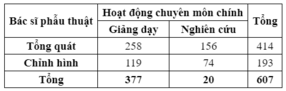

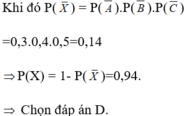
Chọn A
Xác suất để cả ba động cơ cùng hoạt động không tốt là: 0,1.0,2.0,3 = 0,006.
Suy ra, xác suất để có ít nhất một động cơ hoạt động tốt là 1 – 0,006 = 0,994