Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
\(\left\{{}\begin{matrix}a=5c+1\\b=5d+2\end{matrix}\right.\)
\(a^2+b^2=\left(5c+1\right)^2+\left(5d+2\right)^2\)
\(=25c^2+10c+1+25d^2+20d+4\)
\(=25c^2+25d^2+10c+20d+5\)
\(=5\left(5c^2+5d^2+2c+4d+1\right)⋮5\)
Bài 3:
a: \(4x^2+12x+15=4x^2+12x+9+6=\left(2x+3\right)^2+6>=6\forall x\)
Dấu '=' xảy ra khi x=-3/2
b: \(9x^2-6x+5=9x^2-6x+1+4=\left(3x-1\right)^2+4>=4\forall x\)
Dấu '=' xảy ra khi x=1/3

Bài 3:
a) Ta có: \(A=25x^2-20x+7\)
\(=\left(5x\right)^2-2\cdot5x\cdot2+4+3\)
\(=\left(5x-2\right)^2+3>0\forall x\)(đpcm)
d) Ta có: \(D=x^2-2x+2\)
\(=x^2-2x+1+1\)
\(=\left(x-1\right)^2+1>0\forall x\)(đpcm)
Bài 1:
a) Ta có: \(A=x^2-2x+5\)
\(=x^2-2x+1+4\)
\(=\left(x-1\right)^2+4\ge4\forall x\)
Dấu '=' xảy ra khi x=1
b) Ta có: \(B=x^2-x+1\)
\(=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)

Bài 13:
1: \(A=-x^2+4x+3\)
\(=-\left(x^2-4x-3\right)=-\left(x^2-4x+4-7\right)\)
\(=-\left(x-2\right)^2+7\le7\)
Dấu '=' xảy ra khi x=2
2: \(B=-\left(x^2-6x+11\right)\)
\(=-\left(x-3\right)^2-2\le-2\)
Dấu '=' xảy ra khi x=3

Điều kiện x ≠ -2 và x ≠ 0
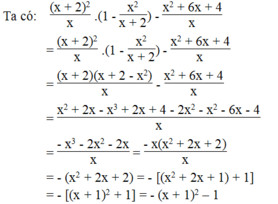
Vì x + 1 2 ≥ 0 nên - x + 1 2 ≤ 0 ⇒ - x + 1 2 - 1 ≤ - 1
Khi đó biểu thức có giá trị lớn nhất bằng -1 khi x = -1
Vậy biểu thức đã cho có giá trị lớn nhất bằng -1 tại x = -1.

Điều kiện x ≠ 2 và x ≠ 0
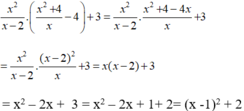
Vì x - 1 2 ≥ 0 nên x - 1 2 + 2 ≥ 2 với mọi giá trị của x.
Khi đó giá trị nhỏ nhất của biểu thức bằng 2 khi x = 1.
Vậy biểu thức đã cho có giá trị nhỏ nhất bằng 2 tại x = 1.
Bài 1
a, Ta có
A = x2 + 6x + 13
⇒ A = (x2 + 6x + 9) + 4
⇒ A = (x + 3)2 + 4
Vì (x + 3)2 ≥ 0 với ∀ x ∈ R
⇒ (x + 3)2 + 4 ≥ 4 > 0 với ∀ x ∈ R
⇒ A > 0 với ∀ x ∈ R (đpcm)
b, B = 2x2 + 4y2 - 4x + 4xy + 13
⇒ B = (2x2 - 4x + 2) + (4y2 + 4xy + 1) + 8
⇒ B = 2 (x2 - 2x + 1) + (2y + 1)2 + 8
⇒ B = 2 (x - 1)2 + (2y + 1)2 + 8
Vì \(\left\{{}\begin{matrix}2\left(x-1\right)^2\ge0\text{ với ∀ x ∈ R}\\\left(2y+1\right)^2\ge0\text{ với ∀ y ∈ R}\end{matrix}\right.\)
⇒ 2 (x - 1)2 + (2y + 1)2 ≥ 0 với ∀ x, y ∈ R
⇒ 2 (x - 1)2 + (2y + 1)2 + 8 ≥ 8 với ∀ x, y ∈ R
⇒ B ≥ 8 với ∀ x, y ∈ R
Dấu " = " xảy ra
⇒ 2 (x - 1)2 + (2y + 1)2 = 0
Mà \(\left\{{}\begin{matrix}2\left(x-1\right)^2\ge0\text{ với ∀ x ∈ R}\\\left(2y+1\right)^2\ge0\text{ với ∀ y ∈ R}\end{matrix}\right.\)
nên : Để 2 (x - 1)2 + (2y + 1)2 = 0
⇒ \(\left\{{}\begin{matrix}2\left(x-1\right)^2=0\text{ }\\\left(2y+1\right)^2=0\text{ }\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}x-1=0\\2y+1=0\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}x=0+1\\2y=0-1\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}x=1\\2y=-1\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}x=1\\y=\dfrac{-1}{2}\end{matrix}\right.\)
Vậy giá trị nhỏ nhất của B là 8 tại \(\left\{{}\begin{matrix}x=1\\y=\dfrac{-1}{2}\end{matrix}\right.\)
Chúc bạn học tốt!!!
cảm ơn bn nhiều nha