Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vẽ tương đối (d1), (d2)
b) Phương trình hoành độ giao điểm của (d1) và (d2):
\(\frac{3}{2}\)\(x+6\)\(=\) \(-3x-3\)
\(\Leftrightarrow\)\(\frac{9}{2}\)\(x=\)\(-9\)
\(\Leftrightarrow\)\(x=\)\(-2\)
\(\Rightarrow\)\(y=3\)
Vậy giao điểm của (d1) và (d2) là \(\left(-2;3\right)\)
c) Gọi phương trình đường thẳng cần tìm là (d): y = ax + b
(d) // (d1) => (d):\(\frac{3}{2}\) \(x+b\)
A \(\in\)(d2) => A \((\)\(\frac{-4}{3}\)\(;1\)\()\)
Thay tọa độ A vào đường thẳng (d) ta có :
1 = \(\frac{3}{2}\) .\(\frac{-4}{3}\)+ b
\(\Leftrightarrow\)b = 3
Vậy (d): y =\(\frac{3}{2}\) \(x+3\)
:3

b: Để hai đường thẳng cắt nhau tại một điểm trên trục tung thì m-1=15
hay m=16

Tình cờ hay cố ý mà dữ liệu bài toán có rất nhiều sự trùng hợp dẫn đến lời giải rất dễ dàng:
\(M\in d_1\Rightarrow y_M=\left(m^2+1\right)x_M-2\Rightarrow y_M+2=\left(m^2+1\right)x_M\)
\(\Rightarrow A=2020\left(m^2+1\right)x_M^2\ge0\)
\(A_{min}=0\) khi \(m=0\)
Khi đó điểm M là \(M\left(0;-2\right)\)

a: 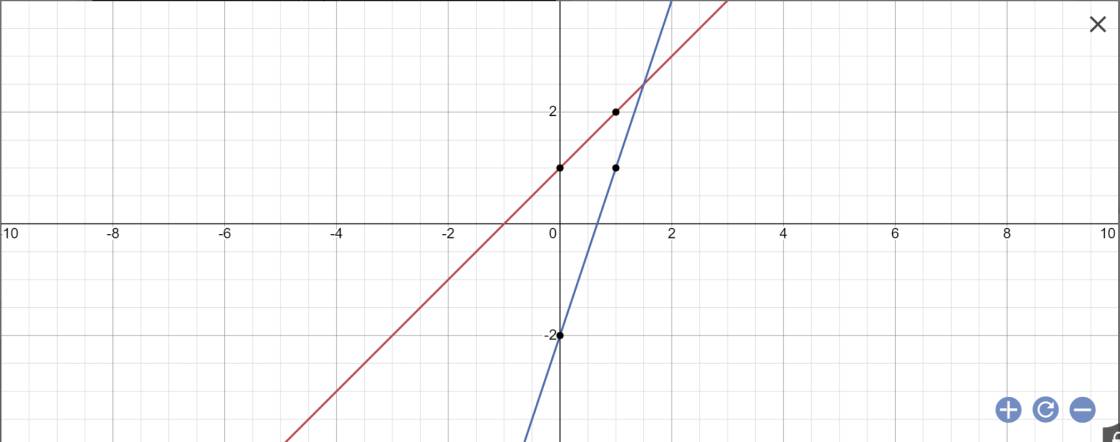
b: Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}3x-2=x+1\\y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-x=2+1\\y=x+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x=3\\y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=\dfrac{3}{2}+1=\dfrac{5}{2}\end{matrix}\right.\)
Thay x=3/2 và y=5/2 vào (d3), ta được:
\(2m+3\cdot\dfrac{3}{2}-1=\dfrac{5}{2}\)
=>\(2m+\dfrac{7}{2}=\dfrac{5}{2}\)
=>\(2m=-1\)
=>m=-1/2
c: (d3): y=2m+3x-1
=>y=m*2+3x-1
Tọa độ điểm mà (d3) luôn đi qua là:
\(\left\{{}\begin{matrix}2=0\left(vôlý\right)\\y=3x-1\end{matrix}\right.\)
=>(d3) không đi qua cố định bất cứ điểm nào
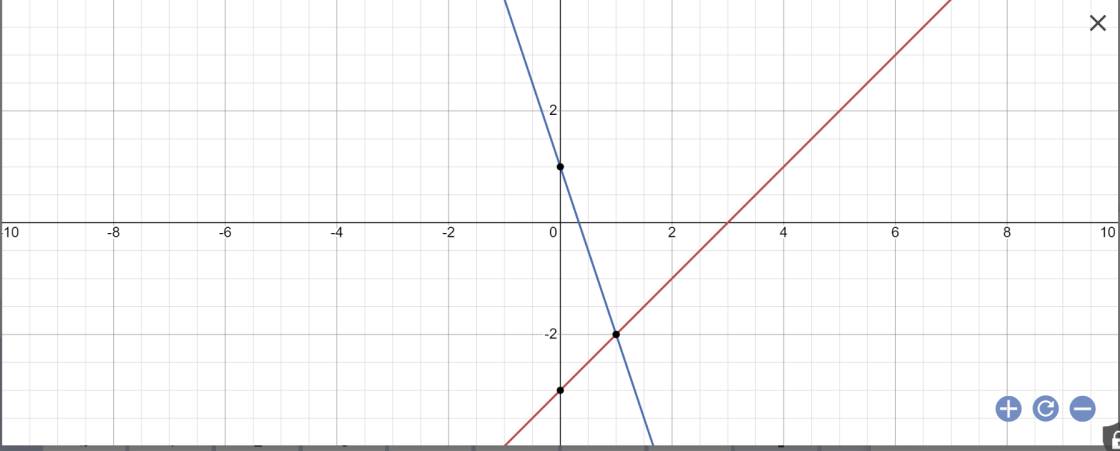

a: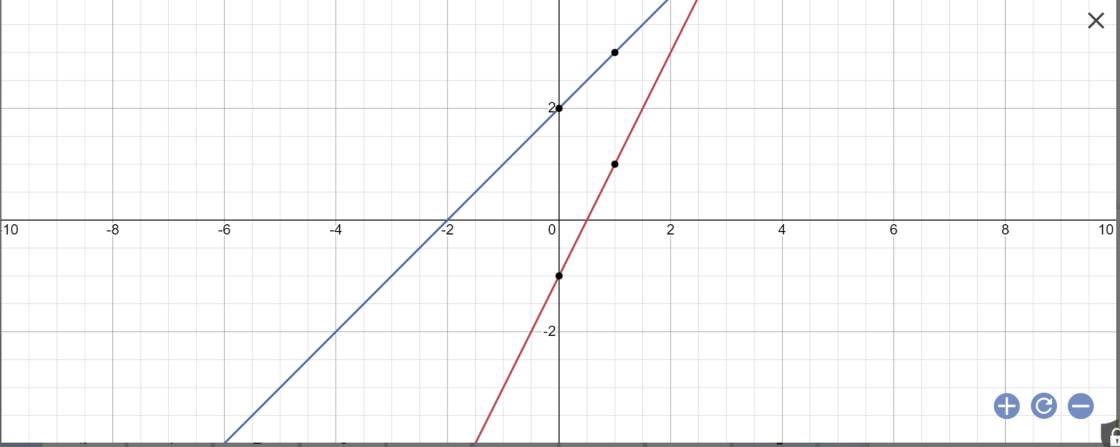
b: Phương trình hoành độ giao điểm là:
2x-1=x+2
=>x=3
Thay x=3 vào y=x+2, ta được:
y=3+2=5
c: Vì (d)//(d1) nên (d): y=2x+b
Thay x=1 và y=0 vào (d), ta được:
b+2=0
=>b=-2
=>y=2x-2