Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

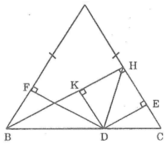
Kẻ DK ⊥ BH
Ta có: BH ⊥AC(gt)
Suy ra: DK // AC (hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song)
⇒ ∠KDB = ∠C (hai góc đồng vị)
VìΔABC cân tại A nên ∠B = ∠C (tính chất tam giác cân)
Suy ra: ∠KDB = ∠B
Xét hai tam giác vuông BFD và DKB, ta có:
∠BFD = ∠DKB = 90o
BD cạnh huyền chung
∠FBD = ∠KDB (chứng minh trên)
Suy ra:ΔBFD=ΔDKB (cạnh huyền góc nhọn)
⇒ DF = BK (hai cạnh tương ứng)(1)
Nối DH. Xét ΔDEH và ΔHKD, ta có:
∠DEH = ∠DKH = 90o
DH cạnh huyền chung
∠EHD = ∠KDH (hai góc so le trong)
Suy ra:ΔDEH = ΔDKH( cạnh huyền , góc nhọn)
Suy ra: DE = HK ( hai cạnh tương ứng) (2)
Mặt khác: BH = BK + KH (3)
Từ (1), (2) và (3) suy ra: DF + DE = BH

Kẻ DK vuông góc BH
Tứ giác DKFE có K=H=E = 90 => DKFE là hình chữ nhật
=> DE = KH (1)
Có DK//AC ( cùng vuông góc với BH ) => góc KDB=ACB
mà ABC=ACB ( tam giác ABC cân )
=> góc KDB = ABC
Xét tam giác BDF và DBK
có F=K=90
góc KDB=ABC
cạnh BD chung
=> tam giác BDF = DBK (ch-gn)
=> BK=DF (2)
có BK+KH=BH (3)
từ (1), (2) và (3) => DE+DF=BH
Lời giải:
Bài 1:
Gọi H là giao điểm của AB và CD
Nối AC, AD,BC,BD
Xét ΔACD và ΔBCD, ta có:
AC = BC
(bán kính hai cung tròn bằng nhau)
AD = BD
CD cạnh chung
Suy ra: ΔACD= ΔBCD(c.c.c)
Suy ra: ∠C2 =∠C2 (hai góc tương ứng)
Xét hai tam giác AHC và BHC. Ta có:
AC = BC (bán kính hai cung tròn bằng nhau)
∠C2 =∠C2 (chứng minh trên)
CH cạnh chung
Suy ra: ΔAHC= ΔBHC(c.g.c)
Suy ra: AH = BH (hai cạnh tương ứng) (1)
Ta có : ∠H1 =∠H2 (hai góc tương ứng)
∠H1 + ∠H2 =180° (hai góc kề bù)
Suy ra: ∠H1 =∠H2 =90° => CD ⊥ AB (2)
Từ (1) và (2) suy ra CD là đường trung trực của AB
bài 2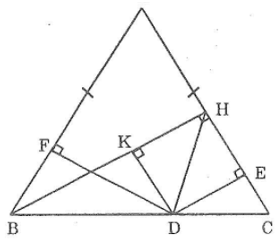
Kẻ DK ⊥ BH
Ta có: BH ⊥AC(gt)
Suy ra: DK // AC (hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song)
=> ∠KDB =C (hai góc đồng vị)
VìΔABC cân tại A nên ∠B =∠C (tính chất tam giác cân)
Suy ra: ∠KDB =B
Xét hai tam giác vuông BFD và DKB, ta có:
∠BFD =∠DKB
BD cạnh huyền chung
∠FBD =∠KDB (chứng minh trên)
Suy ra:ΔBFD=ΔDKB(cạnh huyền góc nhọn)
=> DF = BK (hai cạnh tương ứng)(1)
Nối DH. XétΔDEHvàΔDKH, ta có:
∠DEH =∠DKH =90°
DH cạnh huyền chung
∠EHD =∠KDH (hai góc so le trong)
Suy ra:ΔDEH=ΔDKH( cạnh huyền , góc nhọn)
Suy ra: DE = HK ( hai cạnh tương ứng) (2)
Mặt khác : BH = BK + KH (3)
Từ (1), (2) và (3) suy ra: DF = DE = BH