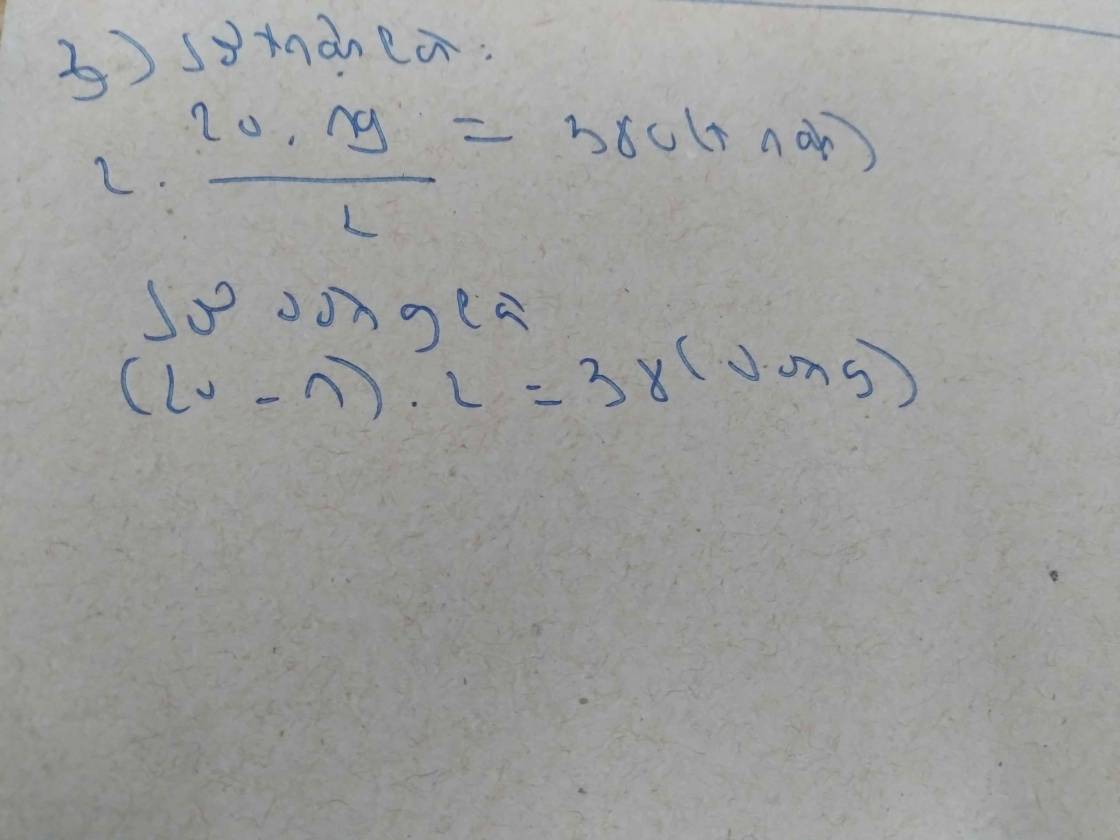Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có 26 chữ cái tiếng Anh và 10 chữ số (từ 0 đến 9).
a) Để tạo một mã bưu chính, ta thực hiện sáu hành động liên tiếp: chọn chữ cái đầu tiên, chọn chữ số thứ hai, chọn chữ cái thứ ba, chọn chữ số thứ tư, chọn chữ cái thứ năm và chọn chữ số thứ sáu.
Mỗi chữ cái được chọn từ 26 chữ cái tiếng Anh nên có 26 cách chọn một chữ cái.
Mỗi chữ số được chọn từ 10 chữ số nên có 10 cách chọn một chữ số.
Vậy có thể tạo được 26 . 10 . 26 . 10 . 26 . 10 = 17 576 000 mã bưu chính.
b) Để tạo một mã bưu chính bắt đầu bằng chữ S, ta thực hiện sáu hành động liên tiếp: chọn chữ cái đầu tiên là S, chọn chữ số thứ hai, chọn chữ cái thứ ba, chọn chữ số thứ tư, chọn chữ cái thứ năm và chọn chữ số thứ sáu.
Chữ cái đầu tiên là S: có 1 cách chọn.
Chọn các chữ cái còn lại, mỗi vị trí có 26 cách chọn.
Chọn các chữ số, mỗi vị trí có 10 cách chọn.
Vậy có thể tạo được 1 . 10 . 26 . 10 . 26 . 10 = 676 000 mã bắt đầu bằng chữ S.
c) Để tạo một mã bưu chính bắt đầu bằng chữ S và kết thúc bằng chữ số 8, ta thực hiện sáu hành động liên tiếp: chọn chữ cái đầu tiên là S, chọn chữ số thứ hai, chọn chữ cái thứ ba, chọn chữ số thứ tư, chọn chữ cái thứ năm và chọn chữ số thứ sáu là chữ số 8.
Chữ cái đầu tiên là S: có 1 cách chọn.
Chọn các chữ cái còn lại, mỗi vị trí có 26 cách chọn.
Chọn chữ số thứ sáu (kết thúc) là 8: có 1 cách chọn.
Chọn các chữ số còn lại, mỗi vị trí có 10 cách chọn.
Vậy có thể tạo được 1 . 10 . 26 . 10 . 26 . 1 = 67 600 mã bắt đầu bằng chữ S và kết thúc bằng chữ số 8.

Các bộ số có thể là (0;3;6); (0;1;5); (0;4;8); (0;1;8); (0;4;5); (1;3;5); (1;3;8); (1;5;6); (3;4;5); (3;4;8); (4;6;8)
Với các bộ (0;3;6); (0;1;5); (0;4;8); (0;1;8); (0;4;5) thì có thể lập được:
\(2\cdot2\cdot1\cdot5=20\left(số\right)\)
Với các bộ còn lại thì lập được 3!*6=6*6=36 số
=>Có 20+36=56 số

Các số tự nhiên nhỏ hơn 1000 gồm các số có 1 chữ số, có 2 chữ số hoặc 3 chữ số.
+ Số có 1 chữ số chia hết cho 5 là: 0 và 5 => có 2 số.
+ Số có 2 chữ số chia hết cho 5:
Hàng đơn vị là 0: chữ số hàng chục có 9 cách chọn.
Hàng đơn vị là 5: chữ số hàng chục có 8 cách chọn (khác 0).
=> Có \(9 + 8 = 17\) (số)
+ Số có 3 chữ số chia hết cho 5:
Hàng đơn vị là 0: chữ số hàng trăm có 9 cách chọn, hàng chục có 8 cách chọn.
Hàng đơn vị là 5: chữ số hàng trăm có 8 cách chọn, hàng chục có 8 cách chọn.
=> Có 9.8+8.8 = 136 (số)
Vậy có tất cả \(2 + 17 + 136 = 155\) số thỏa mãn ycbt.

a: \(\overline{abcd}\)
a có 7 cách chọn
b có 6 cách
c có 5 cách
d có 4 cách
=>Có 7*6*5*4=840 cách
b: Bộ ba chia hết cho 9 sẽ có thể là (1;2;6); (1;3;5); (2;3;4)
Mỗi bộ có 3!=6(cách)
=>Có 6*3=18 cách
c: \(\overline{abcde}\)
e có 3 cách
a có 6 cách
b có 5 cách
c có 4 cách
d có 3 cách
=>Có 3*6*5*4*3=1080 cách

\(\overline{abcde}\)
TH1: e=0
e có 1 cách chọn
Chữ số 2 có 4 cách chọn
ba chỗ còn lại có 4*3*2=24 cách
=>Có 4*24=96 cách
TH2: e=5; a=2
a,e có 1 cach
b có 4 cách
c có 3 cách
dcó 2 cách
=>Có 4*3*2=24 cách
TH3: e=5; a<>2
e có 1 cách chọn
a có 3 cách chon
số 2 có 3 cách
hai số còn lại có 3*2=6 cách
=>Có 3*3*6=54 cách
=>CÓ 96+24+54=174 số

TH1: chữ số tận cùng là 0
Chọn 1 chữ số khác 0 và 2: có 6 cách
Hoán vị 2 chữ số hàng trăm và chục: \(2!\) cách
\(\Rightarrow6.2=12\) số
TH2: chữ số tận cùng là 5
Chọn 1 chữ số khác 2 và 5:
- Nếu chữ số đó là 0: có 1 số \(205\) thỏa mãn
- Nếu chữ số đó khác 0: có 5 cách chọn, hoán vị nó với 2 có 2 cách \(\Rightarrow2.5=10\) số
Tổng cộng: \(12+1+10=23\) số