Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Xét tam giác AME và tam giác BMC, có:
góc AME = góc BMC ( đối đỉnh)
EM = MC ( giải thiết )
AM= MB ( M là trung điểm của AB )
\(\Rightarrow\) TAm giác AME = tam giác BMC ( c-g-c)
\(\Rightarrow\)góc AEM = góc BCM ( hai góc tương ứng)
\(\Rightarrow AE\)//\(BC\) ( đpcm)
Xét tam giác ABC, có: N là trung điểm AC
}
M là trung điểm AB
=> MN là đườg trung bình tam giác ABC
=> MN//BC (1)
Chứng minh tương tự ta có : MN là đường trung bình tam giác AEC
=> MN //AE (2)
{
MN=1/2AE (3)
Từ (1) và (2) => AE//BC (đpcm)
b) Xét tam giác ABF, có : M là trung điểm AB
}
N là trung điểm BF (NF=NB)
=> MN là đường trung bình tam giác ABF
=> MN =1/2 AF (4)
Từ (3) và (4) => AE = AF
Mà A nằm giữa E và F
=> A là trung điểm của EF.
Vậy .....................
a: Xét tứ giác ABCQ có
N là trung điểm của AC
N là trung điểm của BQ
Do đó: ABCQ là hình bình hành
Suy ra: AQ//BC và AQ=BC
Xét tứ giác ACBP có
M là trung điểm của AB
M là trung điểm của CP
Do đó: ACBP là hình bình hành
Suy ra: AP//BC và AP=BC
Ta có: AQ//BC
AP//BC
mà AQ,AP có điểm chung là A
nên Q,A,P thẳng hàng
mà AP=AQ
nên A là trung điểm của PQ
b: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC và MN=BC/2
hay MN=PQ/4
=>PQ=4MN
Hình
mk nghĩ đề bài bn vt nhầm rồi đáng lẽ ra là Trên tia đối của tia NB lấy điểm F chứ ! xem lại đề ha
mk vẽ hình rồi tự thực hiện phần sau :3
hc tốt
a: Xét tứ giác AEBC có
M là trung điểm của AB
M là trung điểm của EC
Do đó: AEBC là hình bình hành
Suy ra: AE=BC
b: Xét tứ giác ABCF có
N là trung điểm của AC
N là trung điểm của BF
Do đó: ABCF là hình bình hành
Suy ra: AF=BC
mà AE=BC
nên AE=FA
a: Xét tứ giác AEBC có
M là trung điểm của AB
M là trung điểm của EC
Do đó: AEBC là hình bình hành
Suy ra: AE=BC
b: Xét tứ giác ABCF có
N là trung điểm của AC
N là trung điểm của BF
Do đó: ABCF là hình bình hành
Suy ra: AF=BC
mà AE=BC
nên AE=FA
Trang 2 nek, z là hết mờ hen^^
Trang 1 nek
Xét tứ giác AEBC có
M là trung điểm của đường chéo AB
M là trung điểm của đường chéo CE
Do đó: AEBC là hình bình hành
Suy ra: AE//BC và AE=BC(1)
Xét tứ giác ABCF có
N là trung điểm của đường chéo AC
N là trung điểm của đường chéo BF
Do đó: ABCF là hình bình hành
Suy ra: AF//BC và AF=BC(2)
Từ (1) và (2) suy ra AE=AF
Ta có: AE//BC
AF//BC
mà AE và AF có điểm chung là A
nên E,A,F thẳng hàng
mà AE=AF
nên A là trung điểm của EF
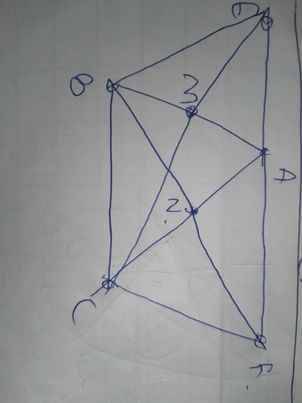
a: Xét ΔAME và ΔBMC có
MA=MB
\(\widehat{AME}=\widehat{BMC}\)(hai góc đối đỉnh)
ME=MC
Do đó: ΔAME=ΔBMC
b: Xét ΔAFN và ΔCBN có
NA=NC
\(\widehat{ANF}=\widehat{CNB}\)(hai góc đối đỉnh)
NF=NB
Do đó: ΔAFN=ΔCBN
c: ΔAME=ΔBMC
=>\(\widehat{MAE}=\widehat{MBC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AE//BC
d: ΔAME=ΔBMC
=>AE=BC
ΔANF=ΔCNB
=>\(\widehat{NAF}=\widehat{NCB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AF//BC
ΔANF=ΔCNB
=>AF=CB
Ta có: AF=CB
AE=BC
Do đó: AE=AF
Ta có: AE//BC
AF//BC
AE,AF có điểm chung là A
Do đó: E,A,F thẳng hàng
mà AE=AF
nên A là trung điểm của EF
Ta có: