Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt A = 22009 + 22008 + ... + 21 + 20. Khi đó, M = 22010 - A
Ta có 2A = 22010 + 22009 + ... + 22 + 21.
Suy ra 2A - A = 22010 - 20 = 22010 - 1.
Do đó M = 22010 - A = 22010 - (22010 - 1) = 22010 - 22010 + 1 = = 1.
M=2^2010-(2^2009+2^2008+2^2007+...+2^1+2^0)
M=22010-22009-22008-22007-...-21-20
=>2M=22011-22010-22009-22008-...-22-21
=>2M-M=22011-22010-22009-22008-...-22-21-(22010-22009-22008-22007-...-21-20)
=>M=22011-22010-22009-22008-...-22-21-22010+22009+22008+22007+...+21+20
=22011-22010-22010+20
=22011-2.22010+1
=22011-22011+1
=1
vậy M=1

3^-200=3^(-2x100)
2^-300=2^(-3x100)
=2^-300>3^-200
chúc bn học tốt
a, 3^(−200) và 2^(−300)
Ta có :
3^(−200) =(3^−2)^100=(1/9)^100
2^(−300) =(2^−3)^100=(1/8)^100
Do 1/9<1/8 nên 3^(−200) < 2^(−300)
b, 33^52 và 44^39
Ta có :
33^52 = ( 33^4)^13
44^39 = ( 44^3 )^13
33^4 = ( 33 4/3 )^3 = 106^3
106^3 > 44^3 ⇒ ( 33^4)^13 > ( 44^3 )^13 ⇒ 33^52 >44^39
#Học tốt#

a) M=
−
1
9
x4y3(2xy2)2=
−
1
9
x4y3(4x2y4)=
−
1
9
x6y7
b) y=
−
x
3
=> x=-3y
mà x+y=2
=>-3y+y=2 <=> -2y=2 => y=-1 => x=-3y=-3*-1=3
Thay x=3; y=-1 vào M...=>M=
−
1
9
(36)(-17)=81
nhớ nhé!

Bài 1:
a) \(=\dfrac{8}{15}\left(\dfrac{7}{13}+\dfrac{6}{13}\right)=\dfrac{8}{15}.1=\dfrac{8}{15}\)
b) \(=\dfrac{3.3-7-2.4}{12}=-\dfrac{6}{12}=-\dfrac{1}{2}\)
Bài 2:
\(\dfrac{x}{2,7}=-\dfrac{2}{3,6}\Rightarrow x=\dfrac{\left(-2\right).2,7}{3,6}\Rightarrow x=-\dfrac{3}{2}\)
Bài 3:
\(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{x+y}{2+5}=-\dfrac{21}{7}=-3\)
\(\Rightarrow\left\{{}\begin{matrix}x=\left(-3\right).2=-6\\y=\left(-3\right).5=-10\end{matrix}\right.\)
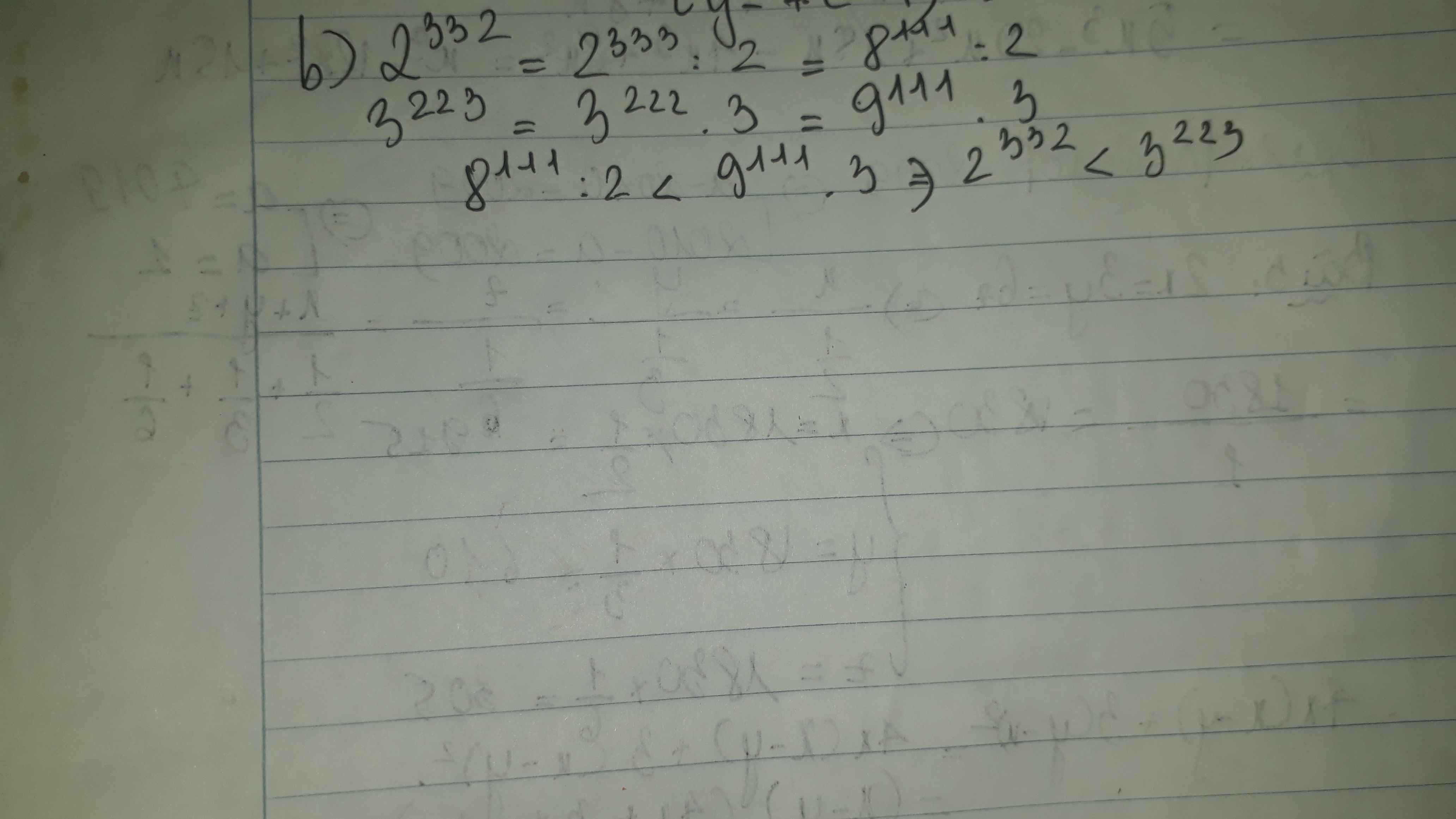

1 , (3/7)^21 :(9/49)^6
= (3/7)^21 : [(3/7)^2]^6
= (3/7)^21 : (3/7)12
= (3/7)^9
2, a) 291 và 535
ta có: 291 < 290 = (25)18 = 3218
lại có: 3218 > 2518 = (52)18 = 536 > 535
vậy 291 > 535
b) 34000 và 92000
ta có: 34000 = (34)1000 = 811000
92000 = (92)1000 = 811000
vậy 34000 = 92000
c) 2332 và 3223
ta có: 2332 < 2333 = (23)111 = 8111
3223 > 3222 = (32)111 = 9111
mà 8111 < 9111
vậy 2332 < 3223
3. n150 = (n2 )75 < 5225 = (53)75 => n2 < 53 = 125 => n2 lớn nhất = 121 => n =11.
4. M=22010-(22009+22008+22007+...+21+20)
M=22010-22009-22008-22007-...-21-20
=>2M=22011-22010-22009-22008-...-22-21
=>2M-M=22011-22010-22009-22008-...-22-21-(22010-22009-22008-22007-...-21-20)
=>M=22011-22010-22009-22008-...-22-21-22010+22009+22008+22007+...+21+20
=22011-22010-22010+20
=22011-2.22010+1
=22011-22011+1
=1
Vậy M=1
\(Bai1:\left(\frac{3}{7}\right)^{21}:\left(\frac{9}{49}\right)^6=\frac{3^{21}}{7^{21}}:\frac{\left(3^2\right)^6}{\left(7^2\right)^6}=\frac{3^{21}}{7^{21}}:\frac{3^{12}}{7^{12}}=\frac{3^{21}}{7^{21}}.\frac{7^{12}}{3^{12}}=\frac{3^9}{7^9}\)
Bài 2: a) 291 = (213)7 = 81927
535 = (55)7 = 31257
Vì 81927 > 31257
=> 291 > 535
b) 34000 = (32)2000 = 92000
=> 34000 = 92000
c) 2332 < 2333 = (23)111 = 8111
3223 > 3222 = (32)111 = 9111
Vì 8111 < 9111
=> 2332 < 3223
Bài 3: n150 < 5225
=> (n2)75 < (53)75
=> n2 < 53
=> n2 < 125
Mà n lớn nhất => n2 lớn nhất => n2 = 121
=> n = 11
Bài 4: Đặt A = 22009 + 22008 + ... + 21 + 20
A = 20 + 21 + ... + 22008 + 22009
2A = 21 + 22 + ... + 22009 + 22010
2A - A = (21 + 22 + ... + 22009 + 22010) - (20 + 21 + ... + 22008 + 22009)
A = 22010 - 20
A = 22010 - 1
=> M = 22010 - (22010 - 1)
M = 22010 - 22010 + 1
M = 1