Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Vì \(AB=AC\) (giả thiết)
\(\Rightarrow\Delta ABC\) cân tại A
Mà \(AM\) là đường trung tuyến (giả thiết)
\(\Rightarrow AM\) cũng là đường phân giác \(\widehat{A}\)
b) Vì \(\Delta ABC\) cân tại A (cmt)
Mà \(AM\) là đường phân giác (cmt)
\(\Rightarrow AM\) là đường trung trực \(BC\)
\(\Rightarrow AM\perp BC\)
c) Xét \(\Delta AMC\left(\widehat{M}=90^o\right)\) có:
\(AC^2=AM^2+MC^2\) (định lí pitago)
\(\Rightarrow AM=\sqrt{AC^2-MC^2}=\sqrt{5^2-\left(\dfrac{6}{2}\right)^2}=4\left(cm\right)\)
d) Xét \(\Delta AME\left(\widehat{E}=90^o\right)\) và \(\Delta AMF\left(\widehat{F}=90^o\right)\) có:
\(\widehat{EAM}=\widehat{FAM}\) (do \(AM\) là tia phân giác \(\widehat{EAF}\))
\(AM\) là cạnh chung
\(\Rightarrow\Delta AME=\Delta AMF\left(ch.gn\right)\)
\(\Rightarrow ME=MF\) (\(2\) cạnh tương ứng)
\(\Rightarrow\Delta MEF\) cân tại \(M\)
a, Xét tam giác ABC có : AB = AC
Vậy tam giác ABC cân tại A
Lại có M là trung điểm BC hay AM là trung tuyến
=> AM đồng thời là đường phân giác ^A
b, Xét tam giác ABC cân tại A
AM là đường trung tuyến đồng thời là đường cao
hay AM vuông BC
c, Vì M là trung tuyến BC => BM = BC/2 = 6/2 = 3 cm
Theo định lí Pytago tam giác ABM vuông tại M
\(AM=\sqrt{AB^2-BM^2}=4cm\)
d, Xét tan giác AFM và tam giác AEM có :
^AFM = ^AEM = 900
AM _ chung
^FAM = ^EAM ( AM là phân giác )
Vậy tam giác AFM = tam giác AEM ( ch - gn )
=> FM = EM ( 2 cạnh tương ứng )
Xét tam giác MEF có FM = EM
Vậy tam giác MEF cân tại M

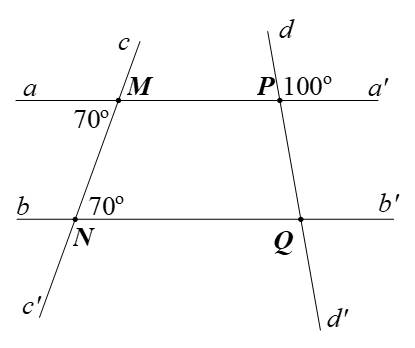
a: Vì góc aMN=góc MNQ
nên aa'//bb'
b: góc PQN=180-100=80 độ=góc b'Qd'
góc b'Qd=d'QN=180-80=100 độ

a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
=>góc BAM=góc CAM
=>AM là phân giác của góc BAC
b: ΔABC cân tại A
mà AM là trung tuyến
nên AM vuông góc BC
c: BM=CM=3cm
=>AM=4cm

a) Xét ΔABC có AB=AC=5
=> ΔABC cân tại A
ta có AM là trung tuyến => AM là đường phân giác của góc A (tc Δ cân)
=>\(\widehat{B}=\widehat{C}\)(tc)
Xét ΔABM và ΔACM có
AB=AC gt
có AM là trung tuyến => BM=CM
\(\widehat{B}=\widehat{C}\) (cmt)
=>ΔABM = ΔACM (cgc)
b) có ΔABC cân
mà AM là trung tuyến => AM là đường cao (tc Δ cân)
c) ta có AM là trung tuyến =>
M là trung điểm của BC
=> BM=CM=\(\dfrac{BC}{2}=\dfrac{6}{2}=3\)cm
Xét ΔABM có AM là đường cao => \(\widehat{AMB}=\)90o
=> AM2+BM2=AB2
=> AM2+32=52
=> AM =4 cm
d) Xét ΔBME và ΔCMF có
\(\widehat{MEB}=\widehat{MFC}=\)90o (ME⊥AB,MF⊥AC)
BM=CM (cmt)
\(\widehat{B}=\widehat{C}\)
=>ΔBME = ΔCMF (ch-cgv)
=>EM=FM( 2 góc tương ứng)
Xét ΔMEF có
EM=FM (cmt)
=> ΔMEF cân tại M

Bài 1:
a)
Góc ở đáy = (180o-50o) : 2 = 65o
b)
Góc ở đỉnh = 180o - (50o x 2) = 80o

a. Xét tam giác AMB và tam giác AMC:
AB = AC
AM chung
BM = CM (trung tuyến AM hạ từ A đến BC)
=> tam giác AMB = tam giác AMC
=> góc BAM = góc CAM (2 góc tương ứng)=>AM là tia phân giác của góc BACb. đề bài bị thiếuc. ta có BM = CM(cma) => BM = CM = \(\dfrac{BC}{2}\)= \(\dfrac{6}{2}\)= 3(cm) Áp dụng định lí Pi-ta-go vào tam giác ABM: AB2 = BM2 + AM2=> AM2 = AB2 - BM2 AM2 = 52 - 32 = 25 - 9 = 16(cm)=> AM = 4 cm

a) Ta có: \(\begin{cases}AM\perp AB\\BN\perp AB\end{cases}\) \(\Rightarrow AM\) // \(BN\)
b) Có \(\widehat{N_3}=\widehat{N_1}=75^o\) (đối đỉnh)
Ta có: \(\widehat{N_1}=\widehat{M_3}=75^o\) (so le trong)
Lai có: \(\widehat{M_1}=\widehat{M_3}=75^o\) (đối đỉnh)
Và: \(\widehat{M^{ }_2}+\widehat{M_3}=180^o\)
\(\Rightarrow\widehat{M_2}+75^o=180^o\)
\(\Rightarrow\widehat{M_2}=180^o-75^o=105^o\)
Mà: \(\widehat{M_4}=\widehat{M_2}=105^o\) (đối đỉnh)
Vì AB cắt AM và BN tạo nên 2 góc vuông có số đo bằng nhau
=> AM // BN
GỌi góc đã cho 75 độ là N4
Vì N1 là góc đối đỉnh của góc N4 mà N4 = 75 độ
=> N1 = N4 = 75 độ
Vì N4 và M3 là 2 góc đồng vị mà N4 = 75 độ
=> N3 = 75 độ
Vì N4 và M2 là 2 góc trong cùng phía bù nhau
=> N4 + M2 = 180 độ
=> M2 = 180 - N4
Thay N4 = 75 độ
=> M2 = 180 - 75 = 105 độ
Vì M1 là đối đỉnh của M3
=> N1 = M3 = 75 độ
Vì M2 là đối đỉnh của M4
=> M2 = M4 = 105 độ
Hai bài giống nhau nhưng lần này ko dùng kề bù nữa mà dùng ngoài cùng phía bù nhau ,ngoài cùng phía bù nhau chỉ dùng đc khi nó song song vs nhau