Sửa đề: F là hình chiếu của E trên AC

a: Xét ΔCAB có

E là trung điểm của CB

EF//AB

=>F là trung điểm của AC

Xét ΔCAB có

E là trung điểm của CB

ED//AC

=>D là trung điểm của AB

Xét ΔABC có EF//AB

nên EF/Ab=CE/CB=1/2

=>EF=1/2AB=DB

Xét tứ giác BDFE có

FE//BD

FE=BD

=>BDFE là hình bình hành

b: Xét ΔABC có AD/AB=AF/AC

nên DF//BC

=>DF//EH

ΔHAC vuông tại H có HF là trung tuyến

nên HF=AC/2

=>HF=ED
Xét tứ giác EHDF có

EH//DF

ED=HF

=>EHDF là hình thang cân

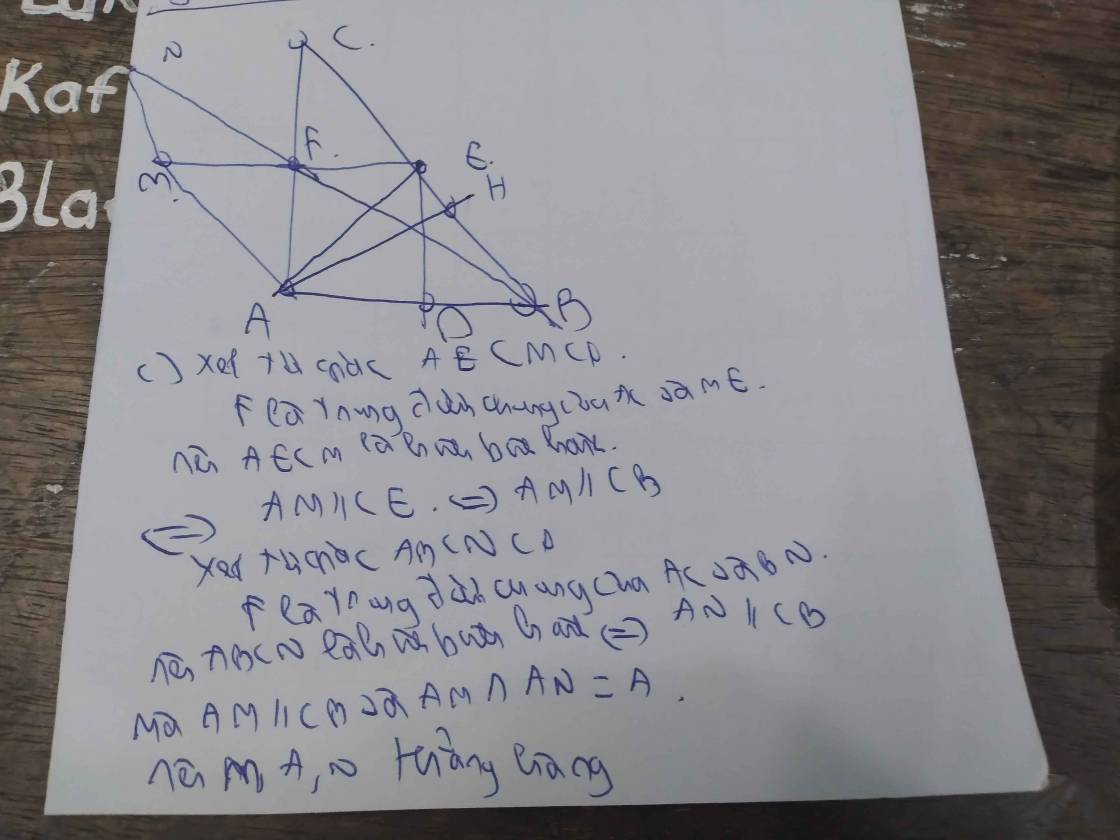
c: Xét tứ giác ABCN có

F là trung điểm chung của AC và BN

=>ABCN là hình bình hành

=>AN//CB

Xét tứ giác AMCE có

F là trung điểm chung của AC và ME

=>AMCE là hình bình hành

=>AM//CE

=>AM//CB

mà AN//CB

nên A,N,M thẳng hàng

Xét ΔABC có

E là trung điểm của BC

EF//AB

Do đó: F là trung điểm của AC

Xét tứ giác AECM có

F là trung điểm của AC 

F là trung điểm của EM

Do đó: AECM là hình bình hành

=>AM//CE

=>AM//CB

Xét tứ giác NMBE có

F là trung điểm chung của NB và ME

=>NMBE là hình bình hành

=>NM//BE

=>NM//BC

AM//BC

NM//BC

mà AM,NM có điểm chung là M

nên M,N,A thẳng hàng

Xét tứ giác 

Cảm ơn nha:))

a: Xét tứ giác ADEF có

góc ADE=góc AFE=góc FAD=90 độ

=>ADEF là hình chữ nhật

b: Xét ΔABC có

E là trung điểm của CB

ED//AC

Do đó: D là trung điểm của AB

Xét ΔABC có

E là trung điểm của CB

EF//AB

Do đó: F là trung điểm của AC

Xét ΔABC có

D,F lần lượt là trung điểm của AB,AC

=>DF là đường trung bình

=>DF//BC và DF=1/2BC

c: DF//BC và DF=1/2BC

mà \(E\in BC;BE=\dfrac{1}{2}BC\)

nên DF//BE và DF=BE

Xét tứ giác BDFE có

DF//BE

DF=BE

Do đó: BDFE là hình bình hành

d: Xét ΔABC có

E là trung điểm của CB

EF//AB

Do đó: F là trung điểm của AC

e: Xét ΔABC có

D,E lần lượt là trung điểm của BA,BC

=>DE là đường trung bình

=>DE=1/2AC

ΔHAC vuông tại H

mà HF là trung tuyến

nên HF=AC/2

=>DE=HF

Xét tứ giác DHEF có

DF//EH

DE=FH

Do đó: DHEF là hình thang cân

Để chứng minh ADEF là hình chữ nhật, ta cần chứng minh các đẳng thức đường cao AH = trung tuyến AE và hình chiếu D, F của E trên AB, AC vuông góc với AB, AC.

a) Chứng minh AH = AE: Vì tam giác ABC là tam giác vuông tại A, nên đường cao AH cũng là đường cao của tam giác vuông ABC. Do đó, ta có AH = BH. Từ tam giác ABC, ta có AE là trung tuyến nên AE = EC. Vậy, AH = AE.

b) Chứng minh AD = AF: Ta có hai tam giác vuông ADE và AFE có cạnh chung AE. Vì AE là trung tuyến nên ta có DE = FE, và góc ADE = góc AFE = 90 độ (do DE và FE vuông góc với AB, AC). Do đó, ta có hai tam giác ADE và AFE đồng dạng (cạnh góc). Từ đó suy ra, AD = AF.

Vì AH = AE và AD = AF, nên tứ giác ADEF là hình chữ nhật.

c) Chứng minh BDFE là hình bình hành: Ta đã chứng minh được AD = AF, nên BD = BF (do AB < AC). Vì DE = EF (vì trung tuyến), và góc EDF = góc EBF = 90 độ (hình chiếu của E trên AB, AC vuông góc với AB, AC), nên ta có hai cạnh và một góc tương đương nhau. Do đó, tứ giác BDFE là hình bình hành.

d) Chứng minh F là trung điểm của AC: Vì AE là trung tuyến của tam giác ABC, nên F là trung điểm của AC.

Vậy, ta đã chứng minh được các yêu cầu đề bài.

Bạn vẽ hình giúp mình nhé!

a. Cm: DFEH là hình thang cân

Xét tam giác AHC vuông tại H có HF là đường trung tuyến ứng với cạnh huyền.

\(\Rightarrow HF=\dfrac{AC}{2}\left(1\right)\) 

Xét tam giác ABC có: \(\left\{{}\begin{matrix}AD=DB\\BE=EC\end{matrix}\right.\)

\(\Rightarrow\)DE là đường trung bình trong tam giác ABC

\(\Rightarrow\) \(DE=\dfrac{AC}{2}\left(2\right)\)

Lại có: Tam giác ABC có: \(\left\{{}\begin{matrix}AD=DB\\AF=FC\end{matrix}\right.\) \(\Rightarrow\)DF là đường trung bình của tam giác ABC

\(\Rightarrow\) DF//BC

\(\Rightarrow\) Tứ giác DFEH là hình thang (3)

Từ (1),(2), và (3) suy ra: DFEH là hình thang cân.

b. Cm: I là trung điểm của DF

Ta có: DFEH là hình thang cân

\(\Rightarrow DE=HF=\dfrac{AC}{2}=AF\)

Mà DE//AC \(\Rightarrow\) DE//AF

\(\Rightarrow\)Tứ giác AFED là hình bình hành

Mà \(I=DF\cap AE\)

\(\Rightarrow\) I là trung điểm của DF

Bài này có gì đâu em ! Anh làm nhé !

Chuyển vế cái cần chứng minh ta được 

1/AB^2 - 1/AE^2 =1/4AF^2

hay ( AE^2 - AB^2)/AB^2.AE^2 = 1/4AF^2

hay BE^2/ 4BC^2.AE^2 = 1/AF^2

Nhân chéo hai vế ta có : BC.AE = BE.AF hay là BC/AF = BE/AE