Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

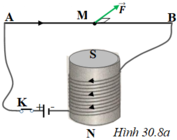
Chọn D. Phương nằm ngang vuông góc với AB, chiều từ ngoài vào trong mặt phẳng hình vẽ.

Để tính lực cực tiểu cần đặt vào đĩa để nhấc (tách) đĩa khỏi đáy bể, ta sẽ sử dụng nguyên lý Pascal và công thức tính áp suất.
Theo nguyên lý Pascal, áp suất được truyền đều trong chất lỏng. Vì vậy, áp suất tại đáy đĩa thép và áp suất tại đáy bể nước phải bằng nhau.
Áp suất tại đáy đĩa thép:
P1 = P0 + ρgh1
Áp suất tại đáy bể nước:
P2 = P0 + ρgh2
Trong đó:
P0 là áp suất khí quyển (105N/m2)
ρ là khối lượng riêng của nước (1g/cm3 = 1000kg/m3)
g là gia tốc trọng trường (10m/s2)
h1 là độ sâu từ đáy bể đến đáy đĩa thép (h1 = 0)
h2 là độ sâu từ đáy bể đến mặt nước (h2 = 0.5m)
Với các giá trị trên, ta có:
P1 = P0 + ρgh1 = 105N/m2 + 1000kg/m3 * 10m/s2 * 0m = 105N/m2
P2 = P0 + ρgh2 = 105N/m2 + 1000kg/m3 * 10m/s2 * 0.5m = 155N/m2
Do áp suất tại đáy đĩa thép và áp suất tại đáy bể nước phải bằng nhau, ta có:
P1 = P2
105N/m2 = 155N/m2
Vậy, lực cực tiểu cần đặt vào đĩa để nhấc (tách) đĩa khỏi đáy bể là 155N.

a, đổi \(a=10cm=0,1m\), \(h2=2cm=0,02m\)
lực đẩy ác si mét lên cả khối gỗ trong dầu và nước
\(=>Fa\left(nuoc\right)+Fa\left(g\right)=Pg\)
\(=>10D1.V1+10D2.V2=10Do.Vg\)
\(=>10000S.h'+8000S.h2=6000S.a\)
\(=>10000h'+8000h2=600\)
\(=>h'=\dfrac{600-8000.0,02}{10000}=0,044m\)
\(\)
b, lúc này khối gỗ chịu t./d của 3 lực acsimet
\(=>\)\(Pg=Fa\left(nuoc\right)+Fa\left(dâu\right)+Fa\left(chat-long\right)\)
\(=>10DoS.h=10000S.\left(0,1-h''\right)+8000S.h2+4000.S.h''\)
\(=>600=10000\left(0,1-h''\right)+8000.0,02+4000h''=>h''\approx0,09m\)

a, Chiều dài nmp:
Ta có: \(h=lsina\)\(\Rightarrow\)\(l=\frac{h}{sina}=\frac{2}{sin30^o}=4m\)
b, Ta có: Công kéo vật = Công thắng trọng lực + Công thắng ma sát:
\(A_k=A_p+A_{ms}\)\(\Rightarrow\)\(A_{ms}=A_k-A_p=F_k.l-P.h=300.4-500.2=200J\)
Lực ma sát : \(F_{ms}=\frac{A_{ms}}{l}=\frac{200}{4}=50N\)
c, Hiệu suất mặt phẳng nghiêng:
\(H=\frac{A_p}{A_k}=\frac{500.2}{300.4}\approx83,33\%\)
kk