Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
a) \(3x^2y-6xy^2\)
\(=3xy\left(x-2y\right)\)
Vậy ...
b) \(\left(2x-a\right)x^2-\left(2x-a\right)y\)
\(=\left(2x-a\right)\left(x^2-y\right)\)
\(=\left(2x-a\right)\left(x-\sqrt{y}\right)\left(x+\sqrt{y}\right)\)
Vậy ...
c) \(25a^2-c^2\)
\(=\left(5a-c\right)\left(5a+c\right)\)
Vậy ...
d) \(4-36x+81x^2\)
\(=2^2-2.2.9x+\left(9x\right)^2\)
\(=\left(2-9x\right)^2\)
Vậy ...
e) \(\left(x+7\right)2-\left(2x-9\right)2\)
\(=2\left[\left(x+7\right)-\left(2x-9\right)\right]\)
\(=2\left(x+7-2x+9\right)\)
\(=2\left(16-x\right)\)
Vậy ...
f) \(x^2-6x+8\)
\(=x^2-6x+9-1\)
\(=\left(x-3\right)^2-1\)
\(=\left(x-4\right)\left(x-2\right)\)
Vậy ...

a.
$x^4-6x^2+9=0$
$\Leftrightarrow (x^2-3)^2=0$
$\Leftrightarrow x^2-3=0$
$\Leftrightarrow x^2=3$
$\Leftrightarrow x=\pm \sqrt{3}$
b.
$8x^3+12x^2+6x-63=0$
$\Leftrightarrow (8x^2+12x^2+6x+1)-64=0$
$\Leftrightarrow (2x+1)^3=64=4^3$
$\Leftrightarrow 2x+1=4$
$\Leftrightarrow x=\frac{3}{2}$
c. $(3-2x)^2-25=0$
$\Leftrightarrow (3-2x)^2-5^2=0$
$\Leftrightarrow (3-2x-5)(3-2x+5)=0$
$\Leftrightarrow (-2-2x)(8-2x)=0$
$\Leftrightarrow -2-2x=0$ hoặc $8-2x=0$
$\Leftrightarrow x=-1$ hoặc $x=4$
d.
$6(x+1)^2-2(x+1)^3+2(x-1)(x^2+x+1)=1$
$\Leftrightarrow (x+1)^2[6-2(x+1)]+2(x^3-1)=1$
$\Leftrightarrow (x+1)^2(4-2x)+2x^3-3=0$
$\Leftrightarrow 6x+1=0$
$\Leftrightarrow x=\frac{-1}{6}$
e. $(x-2)^2-(x-2)(x+2)=0$
$\Leftrightarrow (x-2)[(x-2)-(x+2)]=0$
$\Leftrightarrow (x-2)(-4)=0$
$\Leftrightarrow x-2=0$
$\Leftrightarrow x=2$
f. $x^2-4x+4=25$
$\Leftrightarrow (x-2)^2=5^2=(-5)^2$
$\Leftrightarrow x-2=5$ hoặc $x-2=-5$
$\Leftrightarrow x=7$ hoặc $x=-3$

\(a,\Leftrightarrow9x^2=-36\Leftrightarrow x\in\varnothing\\ b,\Leftrightarrow3\left(x+4\right)-x\left(x+4\right)=0\\ \Leftrightarrow\left(3-x\right)\left(x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\\x=-4\end{matrix}\right.\\ c,\Leftrightarrow2x^2-x-2x^2+3x+2=0\\ \Leftrightarrow2x=-2\Leftrightarrow x=-1\\ d,\Leftrightarrow\left(2x-3-2x\right)\left(2x-3+2x\right)=0\\ \Leftrightarrow-3\left(4x-3\right)=0\\ \Leftrightarrow x=\dfrac{3}{4}\\ e,\Leftrightarrow\dfrac{1}{3}x\left(x-9\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=9\end{matrix}\right.\\ f,\Leftrightarrow x^2\left(x-1\right)-\left(x-1\right)=0\\ \Leftrightarrow\left(x^2-1\right)\left(x-1\right)=0\\ \Leftrightarrow\left(x-1\right)^2\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)

1)(x2-4x+16)(x+4)-x(x+1)(x+2)+3x2=0
\(\Rightarrow\)(x3+64)-x(x2+2x+x+2)+3x2=0
\(\Rightarrow\)x3+64-x3-2x2-x2-2x+3x2=0
\(\Rightarrow\)-2x+64=0
\(\Rightarrow\)-2x=-64
\(\Rightarrow\)x=\(\dfrac{-64}{-2}\)
\(\Rightarrow x=32\)
2)(8x+2)(1-3x)+(6x-1)(4x-10)=-50
\(\Rightarrow\)8x-24x2+2-6x+24x2-60x-4x+10=50
\(\Rightarrow\)-62x+12=50
\(\Rightarrow\)-62x=50-12
\(\Rightarrow\)-62x=38
\(\Rightarrow\)x=\(-\dfrac{38}{62}=-\dfrac{19}{31}\)

a) Ta có: \(36x^3-4x=0\)
\(\Leftrightarrow4x\left(9x^2-1\right)=0\)
\(\Leftrightarrow x\left(3x-1\right)\left(3x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{3}\\x=\dfrac{-1}{3}\end{matrix}\right.\)
b) Ta có: \(3x\left(x-2\right)+x-2=0\)
\(\Leftrightarrow\left(x-2\right)\left(3x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{-1}{3}\end{matrix}\right.\)

a) \(\left(3x-2\right)\left(4x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-2=0\\4x+5=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-\dfrac{5}{4}\end{matrix}\right.\)
Vậy: \(S=\left\{\dfrac{2}{3};-\dfrac{5}{4}\right\}\)
b) \(\left(2,3x-6,9\right)\left(0,1x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2,3x-6,9=0\\0,1x+2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-20\end{matrix}\right.\)
c) \(\left(4x+2\right)\left(x^2+1\right)=0\)
Vì \(x^2+1\ge1>0\forall x\)
\(\Rightarrow4x+2=0\)
\(\Leftrightarrow x=-\dfrac{1}{2}\)
Vậy: \(S=\left\{-\dfrac{1}{2}\right\}\)
d) \(\left(2x+7\right)\left(x-5\right)\left(5x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+7=0\\x-5=0\\5x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{7}{2}\\x=5\\x=-\dfrac{1}{5}\end{matrix}\right.\)
Vậy: \(S=\left\{-\dfrac{7}{2};5;-\dfrac{1}{5}\right\}\)
e) \(\left(x-1\right)\left(2x+7\right)\left(x^2+2\right)=0\)
Vì \(x^2+2\ge2>0\forall x\)
\(\Rightarrow\left(x-1\right)\left(2x+7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\2x+7=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{7}{2}\end{matrix}\right.\)
f) \(\left(3x+2\right)\left(x^2-1\right)=\left(9x^2-4\right)\left(x+1\right)\)
\(\Leftrightarrow\left(3x+2\right)\left(x-1\right)\left(x+1\right)-\left(3x-2\right)\left(3x+2\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[\left(3x+2\right)\left(x+1\right)\right].\left(x-1-3x+2\right)=0\)
\(\Leftrightarrow\left(3x^2+5x+2\right)\left(-2x+1\right)=0\)
\(\Leftrightarrow\left(3x^2+3x+2x+2\right)\left(-2x+1\right)=0\)
\(\Leftrightarrow\left[3x\left(x+1\right)+2\left(x+1\right)\right]\left(-2x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(3x+2\right)\left(-2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\3x+2=0\\-2x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-\dfrac{2}{3}\\x=\dfrac{1}{2}\end{matrix}\right.\)
Vậy: \(S=\left\{-1;-\dfrac{2}{3};\dfrac{1}{2}\right\}\)

\(a,=\left(6x^3+3x^2-10x^2-5x+4x+2\right):\left(2x+1\right)\\ =\left(2x+1\right)\left(3x^2-5x+2\right):\left(2x+1\right)=3x^2-5x+2\\ b,=\left(x^4-2x^3+3x^2+x^3-2x^2+3x\right):\left(x^2-2x+3\right)\\ =\left(x^2-2x+3\right)\left(x^2+x\right):\left(x^2-2x+3\right)=x^2+x\)
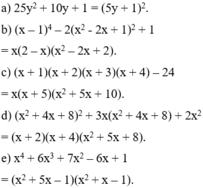

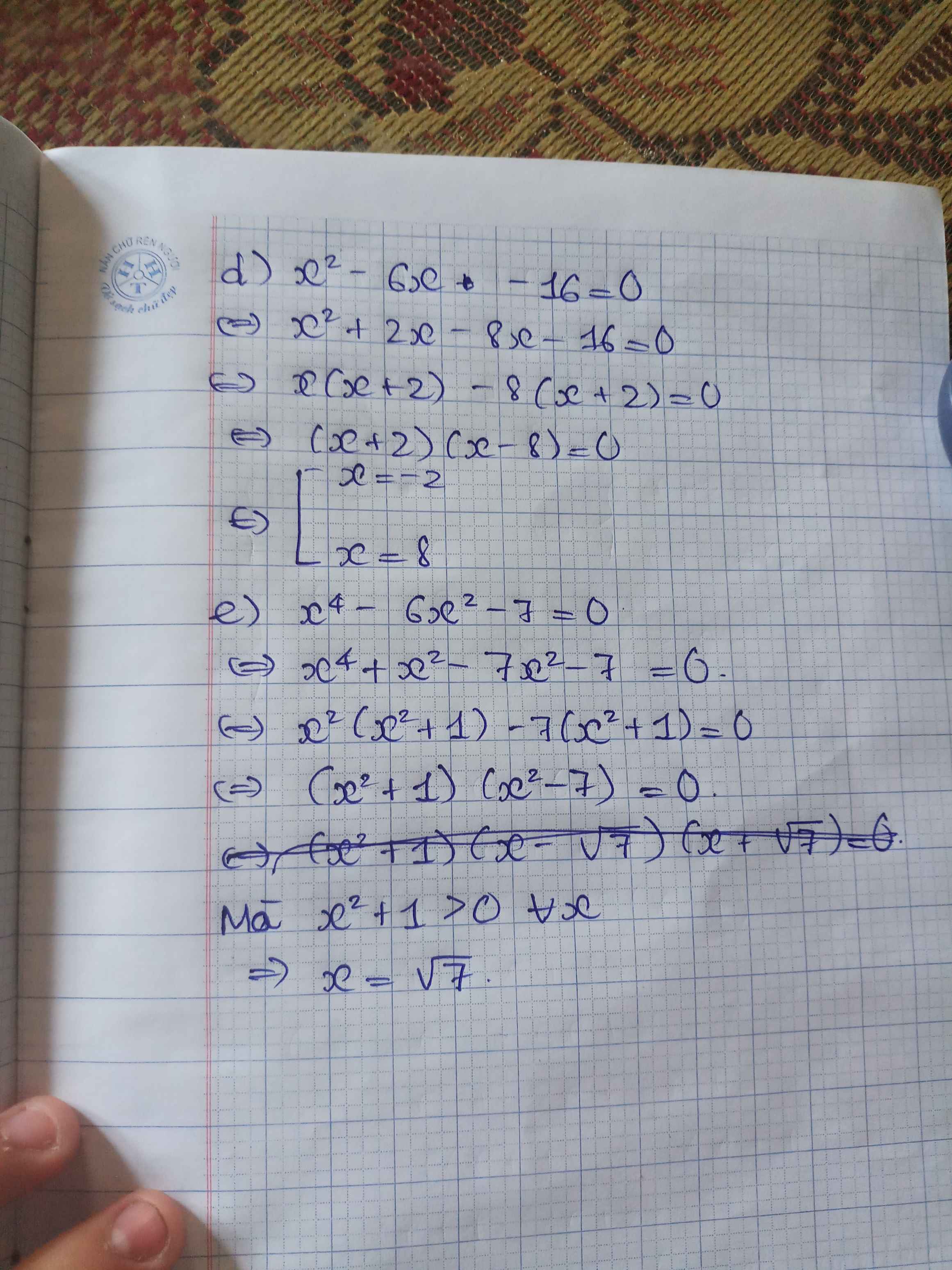

chắc bn nảy hỏi lun cả bài tâp về nhà quá, làm km 1 câu
a) = a+a+a + a +a +1 -a -a -a = a(a+a+1) +(a+a+1) - a(a+a+1)= (a+a+1)(a-a+1)
tự bn thêm mũ 4;3;2 vào được là bn làm dc cac câu sau