Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
+ ω = 2π : T = 20 rad/s.
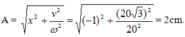
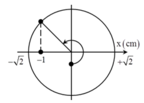
+ t = 0: x = 2cosφ = -1 => 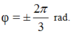
v = -40 sinφ > 0 => sinφ < 0 => ![]()
Vậy: x = 2 cos(20t - 2π/3) = 2 sin(20t - π/6) cm.

+ Độ biến dạng của lò xo tại vị trí cân bằng
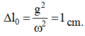
Tại thời điểm t = 0 vật đi qua vị trí cân bằng theo chiều dương. Thời điểm lò xo không biến dạng lần đầu tiên ứng với li độ x = - ∆ l = - 1 cm
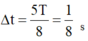
Đáp án D

Gọi \(l\) là chiều dài lò xo lúc ko biến dạng \(\Rightarrow\left\{{}\begin{matrix}l_{max}=l+A=30\\l_{min}=l-A=20\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}l=25cm\\A=5cm\end{matrix}\right.\)
Khi lò xo dài 30cm, tức là vật đang ở biên dương, độ lớn của gia tốc là 8m/s^2\(\Rightarrow\left|a\right|=\omega^2A=800\left(cm/s^2\right)\Leftrightarrow\omega=\sqrt{\dfrac{800}{A}}=\sqrt{\dfrac{800}{5}}=4\pi\left(rad/s\right)\)
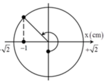
Gốc thời gian là lúc vật qua O theo chiều âm, tức là pha ban đầu bằng pi/2
\(\Rightarrow x=5\cos\left(4\pi t+\dfrac{\pi}{2}\right)\left(cm\right)\)
b/ \(W_d=3W_t\Rightarrow x=\pm\dfrac{A}{\sqrt{3+1}}=\pm\dfrac{A}{2}\)
Nghĩa là khi vật qua vị trí có li độ là \(\left[{}\begin{matrix}x=-2,5cm\\x=2,5cm\end{matrix}\right.\)
c/ Góc vật quay được trong thời gian delta t là: \(\varphi=\omega.\Delta t=4\pi.\Delta t\left(rad\right)\)
Quãng đường lớn nhất đi được khi vật chuyển động xung quanh vtcb
\(S_{max}=2A.\sin\left(2\pi.\Delta t\right)\)
Quãng đường nhỏ nhất đi được khi vật chuyển động xung quang biên
\(S_{min}=2A-2.A\cos\left(2\pi.\Delta t\right)\)
\(\Rightarrow S_{max}-S_{min}=2A\left(\sin\left(2\pi.\Delta t\right)-1+\cos\left(2\pi.\Delta t\right)\right)\)
Xét \(M=\sin\left(2\pi.\Delta t\right)+\cos\left(2\pi.\Delta t\right)=\cos\left(2\pi\Delta t-\dfrac{\pi}{2}\right)+\cos\left(2\pi\Delta t\right)=2\cos\left(\dfrac{2\pi\Delta t-\dfrac{\pi}{2}+2\pi\Delta t}{2}\right)\cos\left(\dfrac{2\pi\Delta t-\dfrac{\pi}{2}-2\pi\Delta t}{2}\right)\)
\(M=2\cos\left(2\pi\Delta t-\dfrac{\pi}{4}\right)\cos\left(\dfrac{\pi}{4}\right)\)
Để \(\left(S_{max}-S_{min}\right)_{max}\Leftrightarrow M_{max}\Leftrightarrow\cos\left(2\pi\Delta t-\dfrac{\pi}{4}\right)=1\)
\(\Leftrightarrow2\pi\Delta t-\dfrac{\pi}{4}=0\Leftrightarrow\Delta t=\dfrac{\pi}{4.2\pi}=\dfrac{1}{8}\left(s\right)\)
d/ Ta thấy vật N luôn dao động vuông pha với vật M
\(\Rightarrow\left(\dfrac{x_M}{A_M}\right)^2+\left(\dfrac{x_N}{A_N}\right)^2=1\Leftrightarrow\left(\dfrac{2,5\sqrt{3}}{5}\right)^2+\left(\dfrac{x_N}{10}\right)^2=1\Leftrightarrow x_N=\pm2,5\left(cm\right)\)
Tính khoảng cách nên ko cần quan tâm xN dương hay âm
\(MN=\sqrt{ON^2+OM^2}=\sqrt{2,5^2+\left(2,5\sqrt{3}\right)^2}=5cm\)

Hướng dẫn:
+ Tần số góc của dao động ω = k m = 10 π rad/s.
Độ biến dạng của lò xo tại vị trí cân bằng Δ l 0 = m g k = 1 c m
+ Khi vật đang ở vị trí có li độ x = –1 cm → l = l 0 = 40 c m , người ta tiến hành giữ cố định lò xo tại điểm cách điểm cố định 20 cm → lò xo mới tham gia vào dao động có độ cứng k' = 2k = 200 N/m.
+ Năng lượng của con lắc trước khi cố định lò xo: E t = k x 2 = 0 , 01 E d = 1 2 k A 2 − x 2 = 0 , 035 J
→ Năng lượng của hệ sau cố định lò xo đúng bằng tổng động năng và một nửa thế năng của vật trước khi cố định lò xo.
E ' = 0 , 5 k A ' 2 = E d + 0 , 5 E t = 0 , 04 J → A' = 0,02 cm.
→ Lực đàn hồi cực đại F m a x = k ' ( 0 , 5 Δ l 0 + A ' ) = 6 N .
Đáp án B
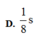



Vì con lắc lò xo nằm ngang nên `\Delta l_0=0`
`=>l_0 =l_[CB]=20(cm)`.