
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đk: x>0, x≠1
P=(√x/(√x -1) +√x/(√x +1)):√(4x)/(x-1)
P=((x+√x)/(x-1)+(x-√x)/(x-1)).(x-1)/√(4x)
P=(x+√x + x-√x)/(x-1).(x-1)/√(4x)
P=(2x)/(x-1).(x-1)/√(4x)
P=(2x)/√(4x)
P=√x
Vậy P=√x

1:
\(A=\sqrt{x^2+\dfrac{2x^2}{3}}=\sqrt{\dfrac{5x^2}{3}}=\left|\sqrt{\dfrac{5}{3}}x\right|=-x\sqrt{\dfrac{5}{3}}\)
2: \(=\left(\dfrac{\sqrt{100}+\sqrt{40}}{\sqrt{5}+\sqrt{2}}+\sqrt{6}\right)\cdot\dfrac{2\sqrt{5}-\sqrt{6}}{2}\)
\(=\dfrac{\left(2\sqrt{5}+\sqrt{6}\right)\left(2\sqrt{5}-\sqrt{6}\right)}{2}\)
\(=\dfrac{20-6}{2}=7\)

Bạn nên gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề và hỗ trợ bạn tốt hơn nhé.

\(A=\sqrt{5-2\sqrt{6}}-\sqrt{\left(\sqrt{2}-\sqrt{3}\right)^2}\)
\(=\sqrt{3}-\sqrt{2}-\sqrt{3}+\sqrt{2}\)
=0


Câu 1:
a. \(\sqrt{x+2}\) có nghĩa khi \(x+2\ge0\Leftrightarrow x\ge-2\)
Vậy biểu thức \(\sqrt{x+2}\) có nghĩa khi \(x\ge-2\)
b. \(\left\{{}\begin{matrix}2x+y=5\\x+2y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+y=5\\2x+4y=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3y=3\\2x+y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1\\x=2\end{matrix}\right.\)
Vậy hệ phương trình có nghiệm duy nhất (x; y) = (2; 1)
c. \(A=\left(\dfrac{3}{x-3\sqrt{x}}+\dfrac{1}{\sqrt{x}+3}\right).\dfrac{x-9}{\sqrt{x}}\left(x>0;x\ne9\right)\)
\(=\left[\dfrac{3\left(\sqrt{x}+3\right)}{\sqrt{x}\left(x-9\right)}+\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\sqrt{x}\left(x-9\right)}\right].\dfrac{x-9}{\sqrt{x}}\)
\(=\dfrac{3\sqrt{x}+9+x-3\sqrt{x}}{\sqrt{x}\left(x-9\right)}.\dfrac{x-9}{\sqrt{x}}\)
\(=\dfrac{x+9}{\sqrt{x}\left(x-9\right)}.\dfrac{x-9}{\sqrt{x}}\)
\(=\dfrac{x+9}{x}\)

\(M=\left(\dfrac{\sqrt{x}}{2x}-\dfrac{1}{\sqrt{x}}\right)\cdot\left(\dfrac{\sqrt{x}-1}{\sqrt{x}+1}-\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\right)\\ =\left(\dfrac{\sqrt{x}}{2x}-\dfrac{2\sqrt{x}}{2x}\right)\cdot\left(\dfrac{\left(\sqrt{x}-1\right)^2-\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\\ =\dfrac{x-2\sqrt{x}}{2x}\cdot\dfrac{x-2\sqrt{x}+1-\left(x+2\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{2x}\cdot\dfrac{x-2\sqrt{x}+1-x-2\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{2x}\cdot\dfrac{-4\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{-2\left(\sqrt{x}-2\right)}{x-1}\)
 bài 2: Rút gọn biểu thức
bài 2: Rút gọn biểu thức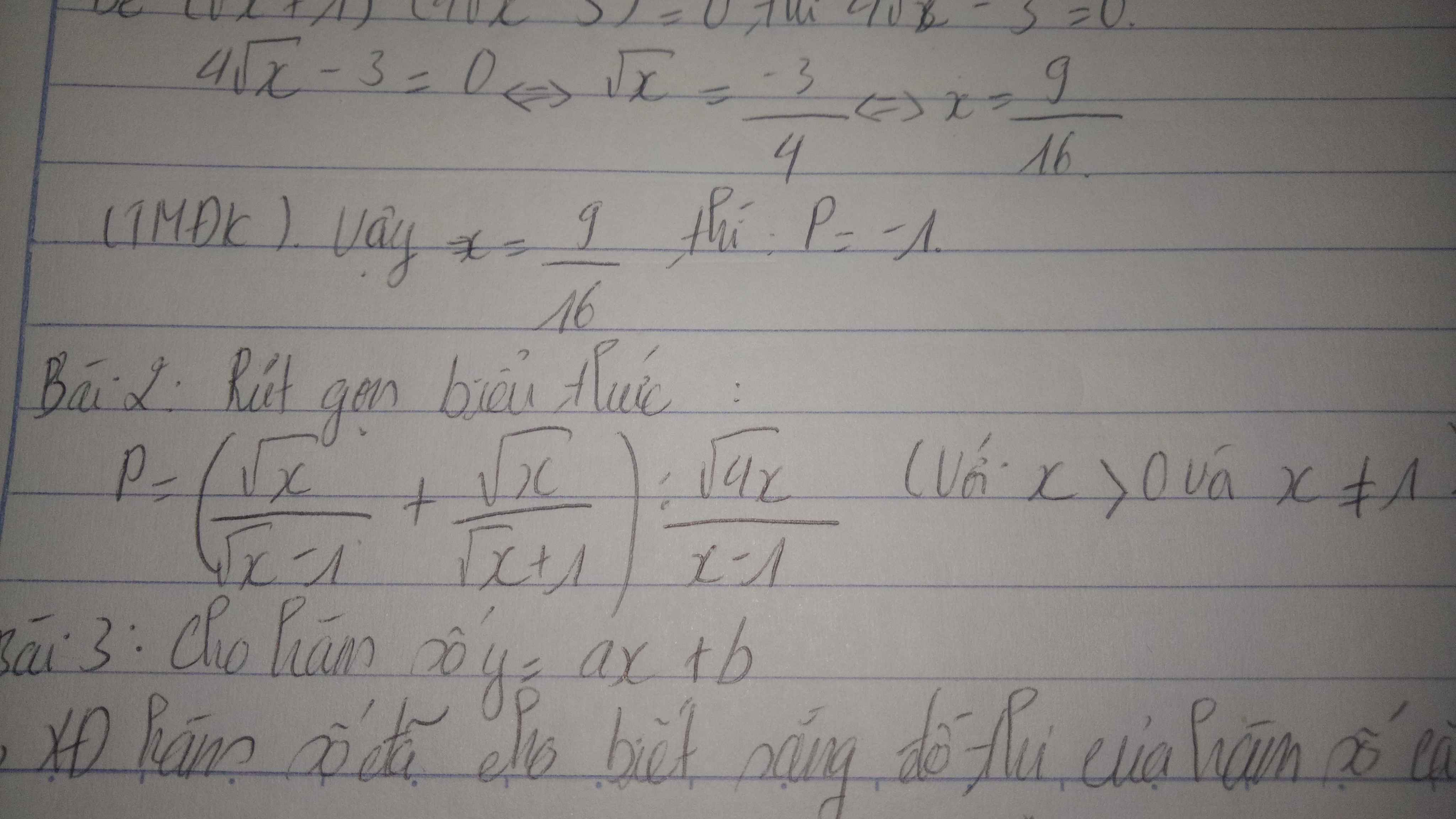

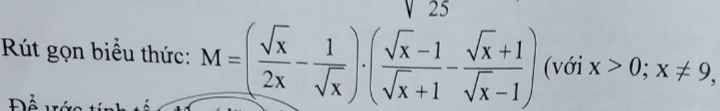
Bài 2 :
a, \(P=\frac{x+2}{\sqrt{x}}+\frac{x\sqrt{x}-1}{x-\sqrt{x}}-\frac{x\sqrt{x}+1}{x+\sqrt{x}}\)Với x > 0 ; \(x\ne1\)
\(=\frac{x+2}{\sqrt{x}}+\frac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}-\frac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(=\frac{x+2+x+\sqrt{x}+1-x+\sqrt{x}-1}{\sqrt{x}}=\frac{x+2\sqrt{x}+2}{\sqrt{x}}\)
b, Ta có : \(P=5\Rightarrow\frac{x+2\sqrt{x}+2}{\sqrt{x}}=5\Rightarrow x+2\sqrt{x}+2=5\sqrt{x}\)
\(\Leftrightarrow x-3\sqrt{x}+2=0\Leftrightarrow\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)=0\Leftrightarrow x=1\left(ktm\right);x=4\left(tm\right)\)