Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(\Leftrightarrow x^2-4-4x^2-4x-1-2x+3x^2=0\)
=>-6x-5=0
=>-6x=5
hay x=-5/6
b: \(\Leftrightarrow2x^3+8x^2+8x-8x^2-2x^3+16=0\)
=>8x+16=0
hay x=-2
c: \(\Leftrightarrow x^3-6x^2+12x-8+9x^2-1-x^3-3x^2-3x-1=0\)
=>9x-10=0
hay x=10/9
d: \(\Leftrightarrow10x-15-20x+28=19-2x^2-4x-2\)
\(\Leftrightarrow-10x+13+2x^2+4x-17=0\)
\(\Leftrightarrow2x^2-6x-4=0\)
\(\Leftrightarrow x^2-3x-2=0\)
\(\text{Δ}=\left(-3\right)^2-4\cdot1\cdot\left(-2\right)=9+8=17>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{3-\sqrt{17}}{2}\\x_2=\dfrac{3+\sqrt{17}}{2}\end{matrix}\right.\)

a, \(12-2\left(1-x\right)^2=\left(3x-2\right)\left(2x-3\right)\)
\(< =>12-2\left(1-2x+x^2\right)=6x^2-9x-4x+6\)
\(< =>12-2+4x-2x^2=6x^2-13x+6\)
\(< =>10+4x-2x^2-6x^2+13x-6=0\)
\(< =>-8x^2+17x+4=0< =>\orbr{\begin{cases}x=\frac{17-\sqrt{417}}{16}\\x=\frac{17+\sqrt{417}}{16}\end{cases}}\)
b, \(10x+3-5x=4x+12< =>5x+3-4x-12=0\)
\(< =>x-9=0< =>x=9\)
c, \(11x+42-2x=100-9x-22< =>9x+42-100+9x+22=0\)
\(< =>18x+64-100=0< =>18x-36=0< =>x=\frac{36}{18}=2\)
d, \(2x-\left(3-5x\right)=4\left(x+3\right)< =>2x-3+5x=4x+12\)
\(< =>7x-3-4x-12=0< =>3x-15=0< =>x=\frac{15}{3}=5\)
e, \(2\left(x-3\right)+5x\left(x-1\right)=5x^2< =>2x-6+5x^2-5=5x^2\)
\(< =>2x-11+5x^2-5x^2=0< =>2x-11=0< =>x=\frac{11}{2}\)
f, \(-6\left(1,5-2x\right)=3\left(-15+2x\right)< =>-6\left(\frac{3}{2}-2x\right)=3\left(2x-15\right)\)
\(< =>-9+12x-6x+45=0< =>6x+36=0< =>x=-6\)
g, \(14x-\left(2x+7\right)=3x+12x-13< =>14x-2x-7=15x-13\)
\(< =>12x-7-15x+13=0< =>-3x+6=0< =>x=-2\)
h, \(\left(x-4\right)\left(x+4\right)-2\left(3x-2\right)=\left(x-4\right)^2\)
\(< =>x^2-16-6x+4=x^2-8x+16\)
\(< =>x^2-6x-12-x^2+8x-16=0\)
\(< =>2x-28=0< =>x=\frac{28}{2}=14\)
q, \(4\left(x-2\right)-\left(x-3\right)\left(2x-5\right)=?\)thiếu đề

a) \(2\chi-3=3\left(\chi+1\right)\)
\(\Leftrightarrow2\chi-3=3\chi+3\)
\(\Leftrightarrow2\chi-3\chi=3+3\)
\(\Leftrightarrow\chi=-6\)
Vậy phương trình có tập nghiệm S= \(\left\{-6\right\}\)
\(3\chi-3=2\left(\chi+1\right)\)
\(\Leftrightarrow3\chi-3=2\chi+2\)
\(\Leftrightarrow3\chi-2\chi=2+3\)
\(\Leftrightarrow\chi=5\)
Vậy phương trình có tập nghiệm S= \(\left\{5\right\}\)
b) \(\left(3\chi+2\right)\left(4\chi-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3\chi+2=0\\4\chi-5=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3\chi=-2\\4\chi=5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\chi=\dfrac{-2}{3}\\\chi=\dfrac{5}{4}\end{matrix}\right.\)
Vậy phương trình có tập nghiệm S= \(\left\{\dfrac{-2}{3};\dfrac{5}{4}\right\}\)
\(\left(3\chi+5\right)\left(4\chi-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3\chi+5=0\\4\chi-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3\chi=-5\\4\chi=2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\chi=\dfrac{-5}{3}\\\chi=\dfrac{1}{2}\end{matrix}\right.\)
Vậy phương trình có tập nghiệm S= \(\left\{\dfrac{-5}{3};\dfrac{1}{2}\right\}\)
c) \(\left|\chi-7\right|=2\chi+3\)
Trường hợp 1:
Nếu \(\chi-7\ge0\Leftrightarrow\chi\ge7\)
Khi đó:\(\left|\chi-7\right|=2\chi+3\)
\(\Leftrightarrow\chi-7=2\chi+3\)
\(\Leftrightarrow\chi-2\chi=3+7\)
\(\Leftrightarrow\chi=-10\) (KTMĐK)
Trường hợp 2:
Nếu \(\chi-7\le0\Leftrightarrow\chi\le7\)
Khi đó: \(\left|\chi-7\right|=2\chi+3\)
\(\Leftrightarrow-\chi+7=2\chi+3\)
\(\Leftrightarrow-\chi-2\chi=3-7\)
\(\Leftrightarrow-3\chi=-4\)
\(\Leftrightarrow\chi=\dfrac{4}{3}\)(TMĐK)
Vậy phương trình có tập nghiệm S=\(\left\{\dfrac{4}{3}\right\}\)
\(\left|\chi-4\right|=5-3\chi\)
Trường hợp 1:
Nếu \(\chi-4\ge0\Leftrightarrow\chi\ge4\)
Khi đó: \(\left|\chi-4\right|=5-3\chi\)
\(\Leftrightarrow\chi-4=5-3\chi\)
\(\Leftrightarrow\chi+3\chi=5+4\)
\(\Leftrightarrow4\chi=9\)
\(\Leftrightarrow\chi=\dfrac{9}{4}\)(KTMĐK)
Trường hợp 2: Nếu \(\chi-4\le0\Leftrightarrow\chi\le4\)
Khi đó: \(\left|\chi-4\right|=5-3\chi\)
\(\Leftrightarrow-\chi+4=5-3\chi\)
\(\Leftrightarrow-\chi+3\chi=5-4\)
\(\Leftrightarrow2\chi=1\)
\(\Leftrightarrow\chi=\dfrac{1}{2}\)(TMĐK)
Vậy phương trình có tập nghiệm S=\(\left\{\dfrac{1}{2}\right\}\)

a,\(4x\left(2x+3\right)-x\left(8x-1\right)=5\left(x+2\right)\)
\(< =>8x^2+12x-8x^2+x=5x+10\)
\(< =>13x=5x+10< =>8x=10\)
\(< =>x=\frac{10}{8}=\frac{5}{4}\)
b, \(\left(3x-5\right)\left(3x+5\right)-x\left(9x-1\right)=4\)
\(< =>9x^2-25-9x^2+x=4\)
\(< =>x=4+29=33\)
c,\(3-4x\left(25-2x\right)=8x^2+x-300\)
\(< =>3-100x+8x^2=8x^2+x-300\)
\(< =>x+100x=3+300\)
\(< =>101x=303< =>x=\frac{303}{101}=3\)
d,\(2\left(1-\frac{3x}{5}\right)-\frac{2+3x}{10}=7-\frac{3\left(2x+1\right)}{4}\)
\(< =>2-\frac{6x}{5}-\frac{2+3x}{10}=7-\frac{6x+3}{4}\)
\(< =>-\frac{24x}{20}-\frac{4+6x}{20}+\frac{30x+15}{20}=5\)
\(< =>\frac{30x-6x-24x+15-4}{20}=5\)
\(< =>\frac{11}{5}=5< =>11=25\)(vo li)
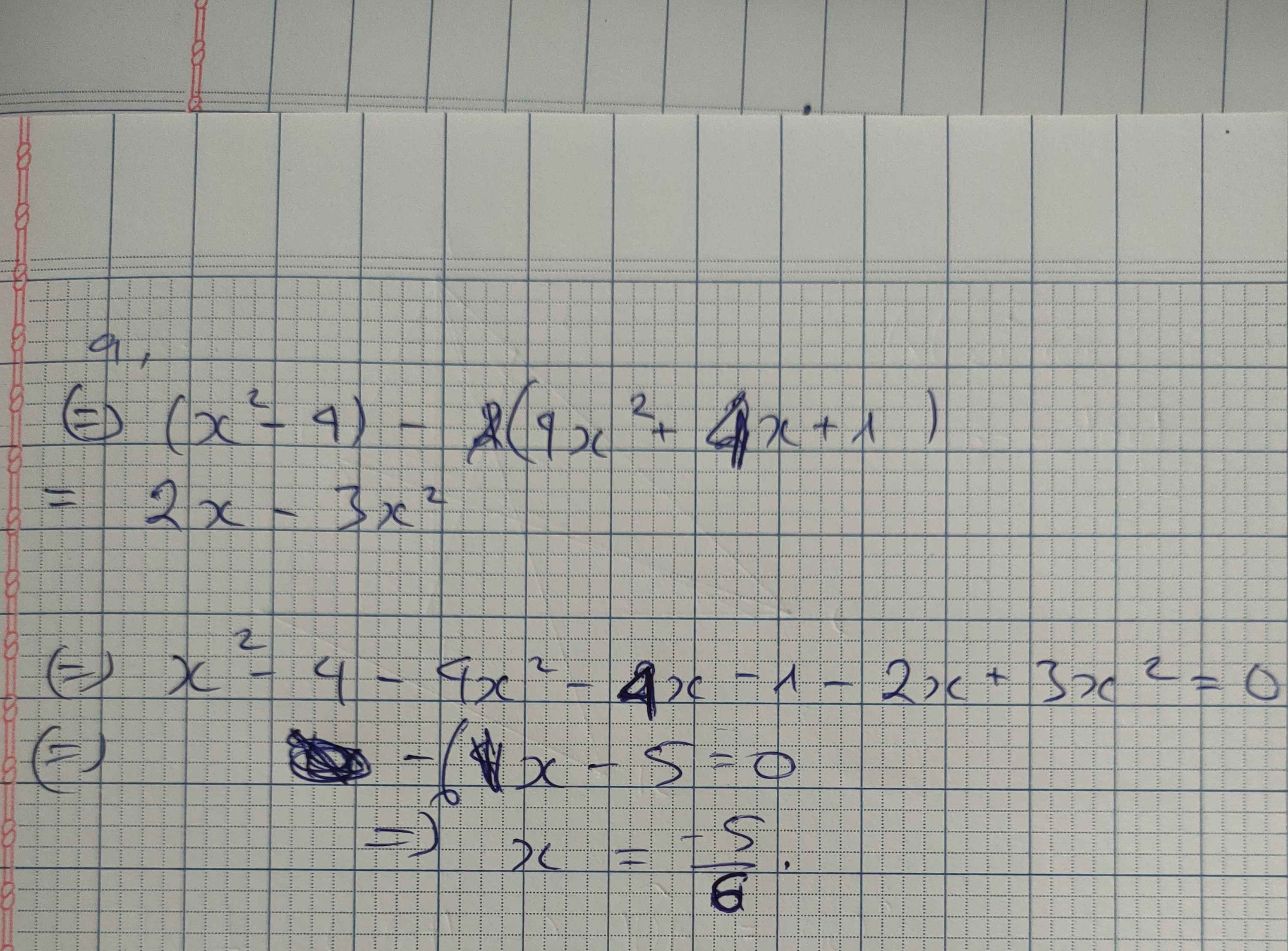
b: \(\Leftrightarrow\dfrac{-3x^2+36x+12}{3\left(x+4\right)\left(x-1\right)}=\dfrac{36\left(x-1\right)}{3\left(x+4\right)\left(x-1\right)}+\dfrac{12\left(x+4\right)}{3\left(x-1\right)\left(x+4\right)}\)
\(\Leftrightarrow-3x^2+36x+12=36x-36+12x+48\)
\(\Leftrightarrow-3x^2+36x+12-48x-12=0\)
\(\Leftrightarrow3x\left(x+4\right)=0\)
=>x=0(nhận) hoặc x=-4(loại)