
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2:
a) xy = -28
\(\Rightarrow\)x, y \(\in\)Ư(-28)
Ta có: Ư(-28) \(\in\){\(\pm\)1; \(\pm\)2; \(\pm\)4; \(\pm\)7; \(\pm\)14; \(\pm\)28}
Lập bảng:
| x | -1 | 1 | -2 | 2 | -4 | 4 | -7 | 7 | -14 | 14 | -28 | 28 |
| y | 1 | -1 | 2 | -2 | 4 | -4 | 7 | -7 | 14 | -14 | 1 | -1 |
b) (2x - 1)(4x + 2) = -42
Câu này bạn lập bảng như câu a
c) x + y +xy = 9
\(\Leftrightarrow\)x(y + 1) + (y + 1) = 10
\(\Leftrightarrow\)(x + 1)(y + 1) = 10
\(\Leftrightarrow\)x + 1 và y + 1 \(\in\)Ư(10)
Ta có: Ư(10) \(\in\){\(\pm\)1; \(\pm\)2; \(\pm\)5; \(\pm\)10}
Lập bảng:
| x + 1 | -1 | 1 | -2 | 2 | -5 | 5 | -10 | 10 |
| y + 1 | 1 | -1 | 2 | -2 | 5 | -5 | 10 | -10 |
| x | -2 | 0 | -3 | 1 | -6 | 4 | -11 | 9 |
| y | 0 | -2 | 1 | -3 | 4 | -6 | 9 | -11 |
d) xy + 3x - 7y = 2
\(\Leftrightarrow\)x(y + 3) - 7y - 21 = -19
\(\Leftrightarrow\)x(y + 3) - 7(y + 3) = -19
\(\Leftrightarrow\)(x - 7)(x + 3) = -19
Tự lập bảng
e) xy - 2x - 3y = 5
\(\Leftrightarrow\)x(y - 2) - 3y + 6 = 11
\(\Leftrightarrow\)x( y - 2) - 3(y - 2) = 11
\(\Leftrightarrow\)(x - 3)(y - 2) = 11
Tự lập bảng
g) xy + 3x -2y = 11
\(\Leftrightarrow\)x(y + 3) - 2y - 6 = 5
\(\Leftrightarrow\)x(y + 3) - 2(y + 3) = 5
\(\Leftrightarrow\)(x - 2)(y + 3) = 5
Tự lập bảng
Bài 1 : Tìm x :
a) (x - 2) (7 - x) > 0
th1 :
x - 2 > 0 và 7 - x > 0
=> x > 2 và -x > -7
=> x > 2 và x < 7
=> 2 < x < 7
th2 :
x - 2 < 0 và 7 - x < 0
=> x < 2 và -x < -7
=> x < 2 và x > 7
=> vô lí
b) (x + 3) (x - 2) < 0
tương tự câu a

1a) (2x - 6)(x + 2) = 0
=> \(\orbr{\begin{cases}2x-6=0\\x+2=0\end{cases}}\)
=> \(\orbr{\begin{cases}2x=6\\x=-2\end{cases}}\)
=> \(\orbr{\begin{cases}x=3\\x=-2\end{cases}}\)
b) (x2 + 7)(x2 - 25) = 0
=> \(\orbr{\begin{cases}x^2+7=0\\x^2-25=0\end{cases}}\)
=> \(\orbr{\begin{cases}x^2=-7\\x^2=25\end{cases}}\)
=> x ko có giá trị vì x2 \(\ge\)0 mà x2= -7
hoặc x = \(\pm\)5

a, \(x,y\in Z\Rightarrow\left\{{}\begin{matrix}x-3,2y-6\in Z\\x-3,2y-6\inƯ\left(5\right)=\left\{\pm1;\pm5\right\}\end{matrix}\right.\)
Ta có bảng:
| x-3 | -1 | -5 | 1 | 5 |
| 2y-6 | -5 | -1 | 5 | 1 |
| x | 2 | -2 | 4 | 8 |
| y | \(\dfrac{1}{2}\left(loại\right)\) | \(\dfrac{5}{2}\left(loại\right)\) | \(\dfrac{11}{2}\left(loại\right)\) | \(\dfrac{7}{2}\left(loại\right)\) |
Vậy không có x,y thỏa mãn đề bài
b, tương tự câu a
\(c,xy-5x+2y=7\\ \Rightarrow x\left(y-5\right)+2y-10=-3\\ \Rightarrow x\left(y-5\right)+2\left(y-5\right)=-3\\ \Rightarrow\left(x+2\right)\left(y-5\right)=-3\)
Rồi làm tương tự câu a
\(d,xy-3x-4y=5\\ \Rightarrow x\left(y-3\right)-4y+12=17\\ \Rightarrow x\left(y-3\right)-4\left(y-3\right)=17\\ \Rightarrow\left(x-4\right)\left(y-3\right)=17\)
Rồi làm tương tự câu a

b) Ta có: \(\left(2x+1\right)\left(3y-2\right)=12\)
\(\Leftrightarrow2x+1\) và 3y-2 là các ước của 12
Trường hợp 1:
\(\left\{{}\begin{matrix}2x+1=1\\3y-2=12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=0\\3y=14\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=\dfrac{14}{3}\end{matrix}\right.\)(loại)
Trường hợp 2:
\(\left\{{}\begin{matrix}2x+1=12\\3y-2=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=11\\3y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{11}{2}\\y=1\end{matrix}\right.\)(loại)
Trường hợp 3:
\(\left\{{}\begin{matrix}2x+1=2\\3y-2=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=1\\3y=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{8}{3}\end{matrix}\right.\)(loại)
Trường hợp 4:
\(\left\{{}\begin{matrix}2x+1=6\\3y-2=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=5\\3y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{2}\\y=\dfrac{4}{3}\end{matrix}\right.\)(loại)
Trường hợp 5:
\(\left\{{}\begin{matrix}2x+1=3\\3y-2=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=2\\3y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)(nhận)
Trường hợp 6:
\(\left\{{}\begin{matrix}2x+1=4\\3y-2=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=3\\3y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=\dfrac{5}{3}\end{matrix}\right.\)(loại)
Trường hợp 7:
\(\left\{{}\begin{matrix}2x+1=-1\\3y-2=-12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=-2\\3y=-10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=\dfrac{-10}{3}\end{matrix}\right.\)(loại)
Trường hợp 8:
\(\left\{{}\begin{matrix}2x+1=-12\\3y-2=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=-13\\3y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{-13}{2}\\y=\dfrac{1}{3}\end{matrix}\right.\)(loại)
Trường hợp 9:
\(\left\{{}\begin{matrix}2x+1=-2\\3y-2=-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=-3\\3y=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{-3}{2}\\y=\dfrac{-4}{3}\end{matrix}\right.\)(loại)
Trường hợp 10:
\(\left\{{}\begin{matrix}2x+1=-6\\3y-2=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=-7\\3y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{-7}{2}\\y=0\end{matrix}\right.\)(loại)
Trường hợp 11:
\(\left\{{}\begin{matrix}2x+1=-3\\3y-2=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=-4\\3y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=-\dfrac{2}{3}\end{matrix}\right.\)(loại)
Trường hợp 12:
\(\left\{{}\begin{matrix}2x+1=-4\\3y-2=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=-5\\3y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{-5}{2}\\y=\dfrac{-1}{3}\end{matrix}\right.\)(loại)
Vậy: (x,y)=(1;2)
Lời giải phần a:
a)
$3xy+9x-2y=10$
$\Leftrightarrow 3x(y+3)-2(y+3)=4$
$\Leftrightarrow (3x-2)(y+3)=4$
Đến đây, do $3x-2,y+3$ đều là số nguyên, $3x-2$ chia $3$ dư $1$ nên ta xét các TH sau:
$3x-2=1; y+3=4\Rightarrow x=1; y=-1$
$3x-2=4; y+3=1\Rightarrow x=2; y=-2$
$3x-2=-2; y+3=-2\Rightarrow x=0; y=-5$
Lời giải:
a. $2y(3x-1)+9x-3=7$
$2y(3x-1)+3(3x-1)=7$
$(3x-1)(2y+3)=7$
Vì $3x-1, 2y+3$ đều là số nguyên với mọi $x,y\in N$, và $2y+3>0$ nên ta có bảng sau:
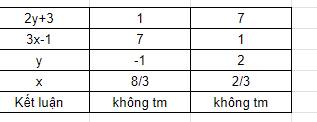
b.
$3xy-2x+3y-9=0$
$x(3y-2)+3y-9=0$
$x(3y-2)+(3y-2)-7=0$
$(3y-2)(x+1)=7$
Đến đây bạn cũng lập bảng tương tự như phần a.