Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,=27-5\sqrt{3x}\\ b,=3\sqrt{2x}-10\sqrt{2x}+21\sqrt{2x}+28=14\sqrt{2x}+28\)

a)
Lưu ý. Các căn số bậc hai là những số thực. Do đó khó làm tính với căn số bậc hai, ta có thể vận dụng mọi quy tắc và mọi tính chất của các phép toàn trên số thực.
b) Dùng phép đưa thừa số ra ngoài dấu căn để có những căn thức giống nhau là .
ĐS:

a) \(2\sqrt{3}-4\sqrt{3x}+27-3\sqrt{3x}\)
= \(\left(2\sqrt{3}+27\right)-\left(4\sqrt{3x}+3\sqrt{3x}\right)\)
=\(\sqrt{3}\left(2+3\right)-\sqrt{3x}\left(4-3\right)\)
=\(5\sqrt{3}-\sqrt{3x}\)
=\(\sqrt{3}\left(5-\sqrt{x}\right)\)
b)\(3\sqrt{2x}-5\sqrt{8x}+7\sqrt{18x}+28\)
=\(3\sqrt{2x}-10\sqrt{2x}+21\sqrt{2x}+28\)
=\(\sqrt{2x}\left(3-10+21\right)+28\)
=\(14\sqrt{2x}+28\)
=\(14\sqrt{2}\left(\sqrt{x}+\sqrt{2}\right)\)

Rút gọn các biểu thức sau với x≥0x≥0:
a) 2\(\sqrt{3x}\)-4\(\sqrt{3x}\)+27-3\(\sqrt{3x}\)=27-5\(\sqrt{3x}\)
b)3\(\sqrt{2x}\)-5\(\sqrt{8x}\)+7\(\sqrt{18x}\)+28
=3\(\sqrt{2x}\)-10\(\sqrt{2x}\)+21\(\sqrt{2x}\)+28
=14\(\sqrt{2x}\)+28=14(\(\sqrt{2x}\)+2)
a) \(2\sqrt{3x}-4\sqrt{3x}+27-3\sqrt{3x}\)
\(=\left(2\sqrt{3x}-4\sqrt{3x}-3\sqrt{3x}\right)+27\)
\(=-5\sqrt{3x}+27\)

a) Ta có: \(A=3\sqrt{2x}-5\sqrt{8x}+7\sqrt{18x}+30\)
\(=3\sqrt{2x}-10\sqrt{2x}+21\sqrt{2x}+30\)
\(=14\sqrt{2x}+30\)
b) Ta có: \(B=4\sqrt{\dfrac{25x}{4}}-\dfrac{8}{3}\sqrt{\dfrac{9x}{4}}-\dfrac{4}{3x}\cdot\sqrt{\dfrac{9x^3}{64}}\)
\(=4\cdot\dfrac{5\sqrt{x}}{2}-\dfrac{8}{3}\cdot\dfrac{3\sqrt{x}}{2}-\dfrac{4}{3x}\cdot\dfrac{3x\sqrt{x}}{8}\)
\(=10\sqrt{x}-4\sqrt{x}-\dfrac{1}{2}\sqrt{x}\)
\(=\dfrac{11}{2}\sqrt{x}\)
c) Ta có: \(\dfrac{y}{2}+\dfrac{3}{4}\sqrt{9y^2-6y+1}-\dfrac{3}{2}\)
\(=\dfrac{1}{2}y+\dfrac{3}{4}\left(1-3y\right)-\dfrac{3}{2}\)
\(=\dfrac{1}{2}y+\dfrac{3}{4}-\dfrac{9}{4}y-\dfrac{3}{2}\)
\(=-\dfrac{7}{4}y-\dfrac{3}{4}\)

9) Sửa: \(2\sqrt{8\sqrt{3}}-2\sqrt{5\text{ }\sqrt{3}}-3\sqrt{20\sqrt{3}}\)
\(=2\sqrt{2^2\cdot2\sqrt{3}}-2\sqrt{5\sqrt{3}}-3\sqrt{2^2\cdot5\sqrt{3}}\)
\(=2\cdot2\sqrt{2\sqrt{3}}-2\sqrt{5\sqrt{3}}-3\cdot2\sqrt{5\sqrt{3}}\)
\(=4\sqrt{2\sqrt{3}}-2\sqrt{5\sqrt{3}}-6\sqrt{5\sqrt{3}}\)
\(=4\sqrt{2\sqrt{3}}-8\sqrt{5\sqrt{3}}\)
10) \(\sqrt{12x}-\sqrt{48x}-3\sqrt{3x}+27\)
\(=\sqrt{2^2\cdot3x}-\sqrt{4^2\cdot3x}-3\sqrt{3x}+27\)
\(=2\sqrt{3x}-4\sqrt{3x}-3\sqrt{3x}+27\)
\(=-5\sqrt{3x}++27\)
11) \(\sqrt{18x}-5\sqrt{8x}+7\sqrt{18x}+28\)
\(=\sqrt{3^2\cdot2x}-5\sqrt{2^2\cdot2x}+7\sqrt{3^2\cdot2x}+28\)
\(=3\sqrt{2x}-5\cdot2\sqrt{2x}+7\cdot3\sqrt{2x}+28\)
\(=3\sqrt{2x}-10\sqrt{2x}+21\sqrt{2x}+28\)
\(=14\sqrt{2x}+28\)
12) \(\sqrt{45a}-\sqrt{20a}+4\sqrt{45a}+\sqrt{a}\)
\(=\sqrt{3^2\cdot5a}-\sqrt{2^2\cdot5a}+4\sqrt{3^2\cdot5a}+\sqrt{a}\)
\(=3\sqrt{5a}-2\sqrt{5a}+4\cdot3\sqrt{5a}+\sqrt{a}\)
\(=3\sqrt{5a}-2\sqrt{5a}+12\sqrt{5a}+\sqrt{a}\)
\(=13\sqrt{5a}+\sqrt{a}\)

Bài 1:
a: \(\sqrt{50}+2\sqrt{8}-\dfrac{3}{2}\cdot\sqrt{72}+\sqrt{125}\)
\(=5\sqrt{2}+2\cdot2\sqrt{2}-\dfrac{3}{2}\cdot6\sqrt{2}+\sqrt{125}\)
\(=9\sqrt{2}-9\sqrt{2}+5\sqrt{5}=5\sqrt{5}\)
b: \(\left(3\sqrt{2}-\sqrt{5}\right)^2-\dfrac{9}{\sqrt{5}-\sqrt{2}}\)
\(=18-2\cdot3\sqrt{2}\cdot\sqrt{5}+5-\dfrac{9\left(\sqrt{5}+\sqrt{2}\right)}{5-2}\)
\(=23-6\sqrt{10}-3\left(\sqrt{5}+\sqrt{2}\right)\)
\(=23-6\sqrt{10}-3\sqrt{5}-3\sqrt{2}\)
c: \(5\sqrt{4a}-3\sqrt{25a}+\sqrt{9a}\)
\(=5\cdot2\sqrt{a}-3\cdot5\sqrt{a}+3\sqrt{a}\)
\(=10\sqrt{a}-15\sqrt{a}+3\sqrt{a}=-2\sqrt{a}\)
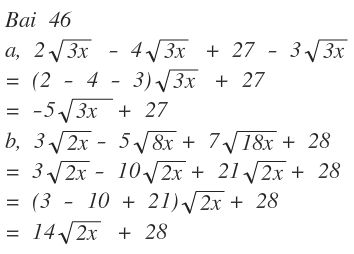
\(a,=27-5\sqrt{3x}\\ b,=3\sqrt{2x}-10\sqrt{2x}+21\sqrt{2x}+28=14\sqrt{2x}+28\)