Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
b: Xét ΔBDF và ΔEDC có
\(\widehat{BDF}=\widehat{EDC}\)
DB=DE
\(\widehat{DBF}=\widehat{DEC}\)
Do đó: ΔBDF=ΔEDC

a, xét tam giác ABD và tam giác AED có : AD chung
^BAD = ^EAD do AD là pg của ^BAC (gt)
AB = AE (gt)
=> tam giác ABD = tam giác AED (c-g-c)
b, tam giác ABD = tam giác AED (câu a)
=> ^ABD = ^AED (đn)
^ABD + ^DBF = 180
^AED + ^DEC = 180
=> ^DBF = ^DEC
xét tam giác FBD và tam giác CED có : BF = EC (gt)
DB = DE do tam giác ABD = tam giác AED (câu a)
=> tam giác FBD = tam giác CED (c-g-c)
c, tam giác FBD = tam giác CED (câu b)
=> ^BDF = ^EDC (đn)
B;D;C thẳng hàng => ^BDE + ^EDC = 180
=> ^BDE + ^BDF = 180
=> E;D;F thẳng hàng
d, AB = AE (gt) => A thuộc đường trung trực của BE (tc)
BD = DE (câu b) => D thuộc đường trung trực của BE (Tc)
=> AD là đường trung trực của BE
e, DF = DC do tam giác BDF = tam giác EDC (Câu b)
=> tam giác DFC cân tại D (đn)
=> ^DCF = (180 - ^FDC) : 2 (tc)
DB = DE (câu b) => tam giác DEB cân tại D (đn) => ^EBD = (180 - ^BDE) : 2 (tc)
^FDC = ^BDE (đối đỉnh)
=> ^DCF = ^EBD mà 2 góc này slt
=> BE // CF

a: Xét ΔABD và ΔAED có
AB=AE
góc BAD=góc EAD
AD chung
Do đó: ΔABD=ΔAED
=>DB=DE
b: Xét ΔDBF và ΔDEC có
góc DBF=góc DEC
DB=DE
góc BDF=góc EDC
Do đo: ΔDBF=ΔDEC
c:ΔDBF=ΔDEC
nên góc BDF=góc EDC
=>góc BDF+góc BDE=180 độ
=>E,D,F thẳng hàng

a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
Suy ra: DB=DE và \(\widehat{ABD}=\widehat{AED}\)
hay \(\widehat{DBF}=\widehat{DEC}\)
Xét ΔDBF và ΔDEC có
\(\widehat{DBF}=\widehat{DEC}\)
DB=DE
\(\widehat{BDF}=\widehat{EDC}\)
Do đó: ΔDBF=ΔDEC

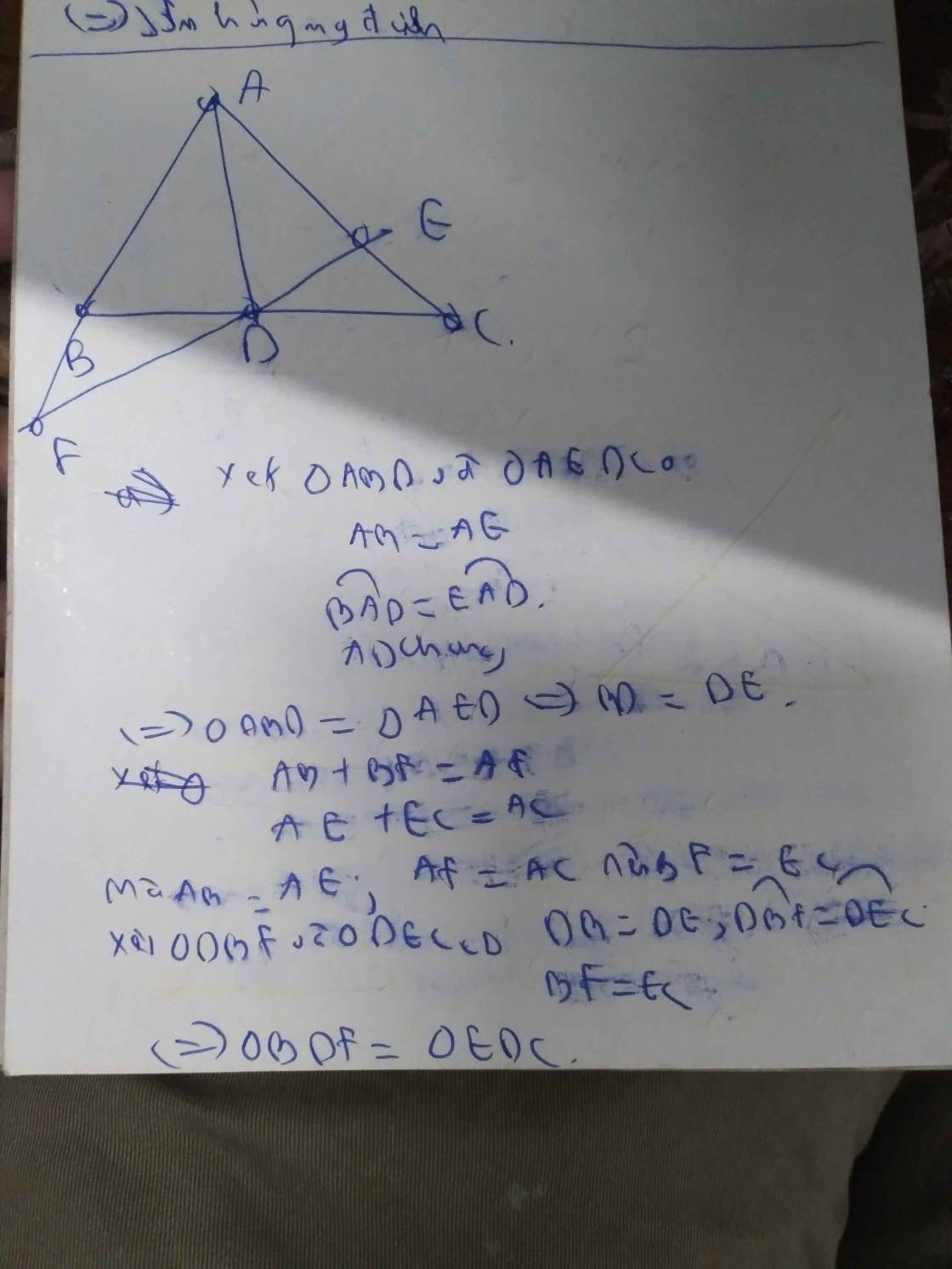
a: Xét ΔADF và ΔADC có
AD chung
\(\widehat{FAD}=\widehat{CAD}\)
AF=AC
Do đó: ΔADF=ΔADC
b: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
=>DB=DE và \(\widehat{ABD}=\widehat{AED}\)
Ta có: \(\widehat{ABD}+\widehat{FBD}=180^0\)(hai góc kề bù)
\(\widehat{AED}+\widehat{CED}=180^0\)(hai góc kề bù)
mà \(\widehat{ABD}=\widehat{AED}\)
nên \(\widehat{FBD}=\widehat{CED}\)
Ta có: AB+BF=AF
AE+EC=AC
mà AB=AE và AF=AC
nên BF=EC
Xét ΔDBF và ΔDEC có
DB=DE
\(\widehat{DBF}=\widehat{DEC}\)
BF=EC
Do đó: ΔDBF=ΔDEC
=>\(\widehat{BDF}=\widehat{EDC}\)
mà \(\widehat{EDC}+\widehat{BDE}=180^0\)(hai góc kề bù)
nên \(\widehat{BDE}+\widehat{BDF}=180^0\)
=>E,D,F thẳng hàng
c: Ta có: ΔDBF=ΔDEC
=>DF=DC
=>D nằm trên đường trung trực của CF(1)
ta có: AF=AC
=>A nằm trên đường trung trực của CF(2)
Từ (1) và (2) suy ra AD là đường trung trực của CF
=>AD\(\perp\)CF