
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1000 ! .( 456 . 789789 - 789 . 456456 )
= 1000 ! x ( 456 x 789 x 1001 - 789 x 456 x 1001 )
= 1000 ! x 0 = 0
1000 ! .( 456 . 789789 - 789 . 456456 )
= 1000 ! x ( 456 x 789 x 1001 - 789 x 456 x 1001 )
= 1000 ! x 0 = 0

Gọi số điểm ban đầu là n.
Ta có công thưc tính số đường thẳng qua n-3 điểm cho sẵn là: (n-3).(n-3-1):2
=(n-3).(n-4):2=36
=>(n-3).(n-4)=72=8.9
=>(n-3).(n-4)=(11-3).(11-4)
=>n=11
=>Ban đầu có 11 điểm.
=>Có số đoạn thẳng là: 11.(11-1):2=11.10:2=1100:2=550
Vậy nếu không bớt 3 điểm thì có 550 đoạn thẳng.

Các số đó là: 10;11;12;13;14;......;19
Các số đó là: 20;22;24;26;28
Các số đó là: 30;33;36;39
Các số đó là: 40;44;48
Cứ như thế nhé

TRả lời :
=1+2+3+...+25=328(có 25 góc tạo bởi 2 tia liên tiêp + 24 góc tạo bởi 2 tia cách nhau 1tia ở giưã +....+1 góc to nhấ cuối cùng)
2/.số chia hêt cho 9 thi tổng các chữ số của nó cũngchia hêt cho 9do vây chỉ có thể viết thêm vào số 3 mà thôi vậy hoán vị đi chỉ có 12 số có 4 chữ số viêt bởi cá số 1;2;3 chia hêt cho :9
3/ số trứng cò lại =1/1-3/7-2=4/7-2=30 hay 4/7=32 suy ra số trứng là 1/1=7/7=7x8=
9/ phân số đó là 7/12- Mẫu số m=tử số :t+5 mà tử số bớt 1là t-1=1/2 mẫu số thế là tìm ra
Bạn giải cách tính ngược nha :
Số trứng khi chưa bán thêm 2 quả là :
30:3/7=70(quả)
Số trứng lúc đầu người đó mang đi là :
70+2=72(quả)
Đ/S: 72 quả

Ta có : 5 : 4 dư 1 suy ra 5 -1 chia hết cho 4
5^2 :4 dư 1 suy ra 5^2 -1 chia hết cho 4
5^3 :4 dư 1 suy ra 5^3 -1 chia hết cho 4
suy ra 5^n : 4 dư 1 suy ra 5^n - 1 chia hết cho 4
Vậy 5^n - 1 chia hết cho 4 với n thuộc N
tk mk nha
5 : 4 dư 1 thì 5n với n thuộc Z chia cho 4 cũng dư 1
=> Vậy nếu 5n - 1 thì tất nhiên Chia hết cho 4

Bài 94:
\(\frac{6}{5}\)= 1\(\frac{1}{5}\)
\(\frac{7}{3}\)= 2\(\frac{1}{3}\)
-\(\frac{16}{11}\)= -1\(\frac{5}{11}\)
tk cho mk nha
6/5=\(1\frac{1}{5}\)
7/3=\(2\frac{1}{3}\)
-16/11=\(-1\frac{5}{11}\)
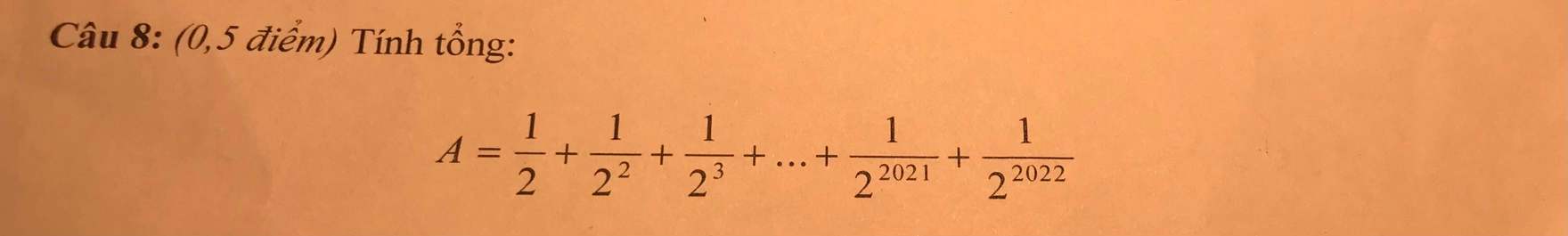 bài khó quá bạn nào là được thì giúp mình
bài khó quá bạn nào là được thì giúp mình
\(2A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2021}}\)
\(2A-A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2021}}-\dfrac{1}{2}-\dfrac{1}{2^2}-...-\dfrac{1}{2^{2022}}=1-\dfrac{1}{2^{2022}}=\dfrac{2^{2022}-1}{2^{2022}}\)
\(\Rightarrow2A=1+\dfrac{1}{2}+....+\dfrac{1}{2^{2021}}\)
\(\Rightarrow2A-A=1+\dfrac{1}{2}+....+\dfrac{1}{2^{2021}}-\dfrac{1}{2}-\dfrac{1}{2^2}-...-\dfrac{1}{2^{2022}}\)
\(\Rightarrow A=1-\dfrac{1}{2^{2022}}\)