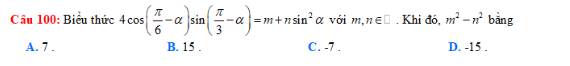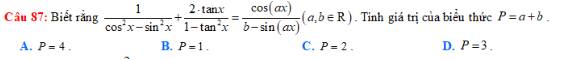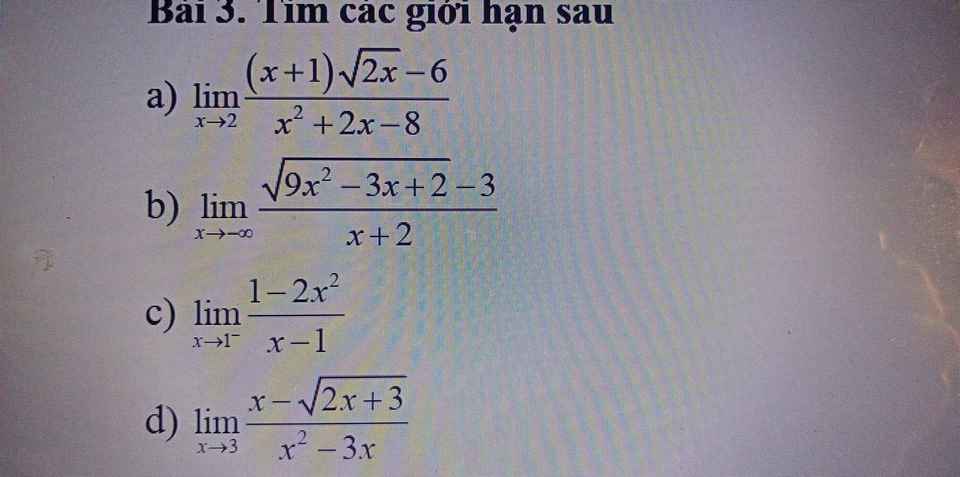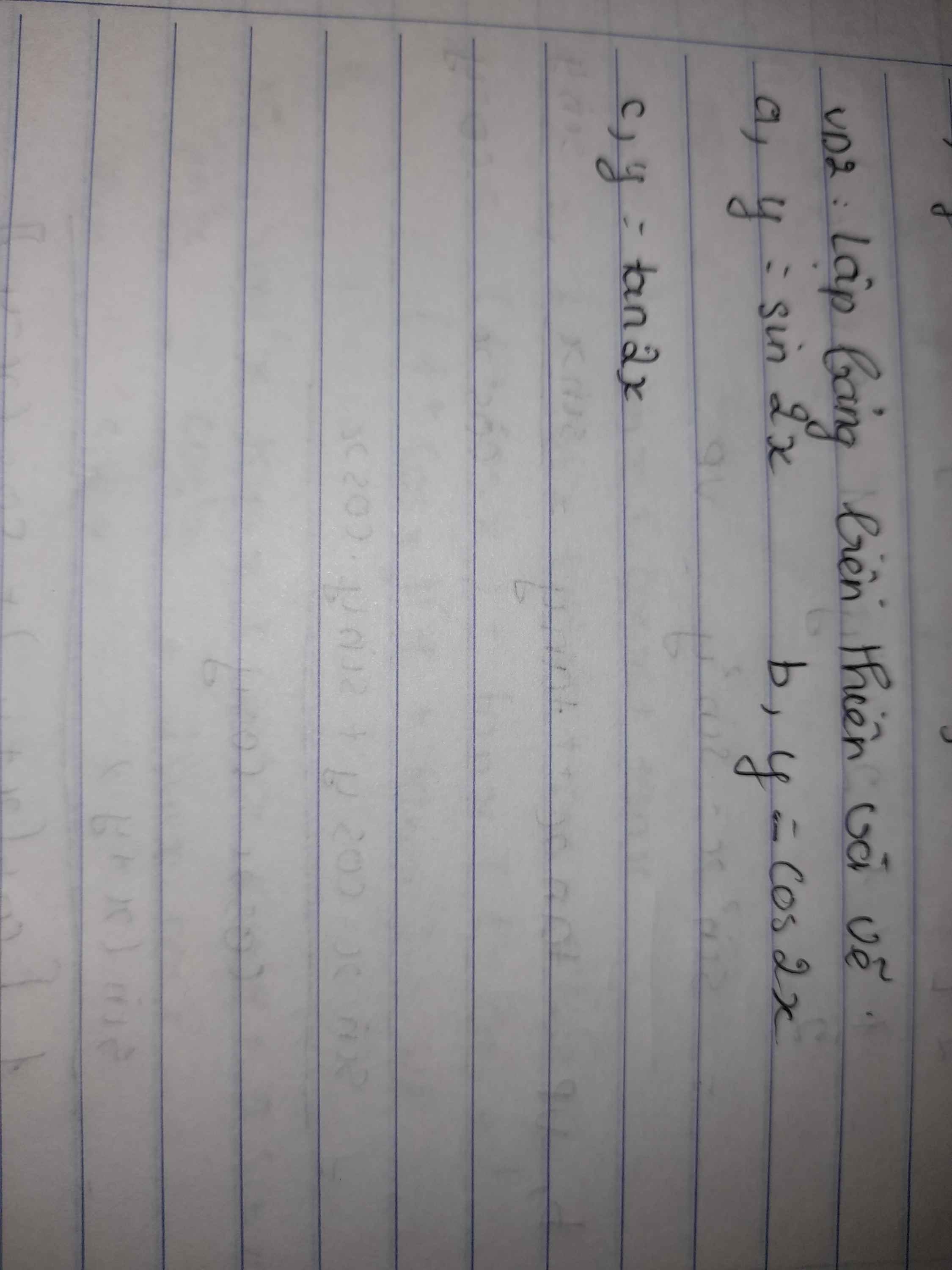4*cos(pi/6-a)*sin(pi/3-a)

=4*(cospi/6*cosa+sinpi/6*sina)*(sinpi/3*cosa-sina*cospi/3)

=4*(căn 3/2*cosa+1/2*sina)*(căn 3/2*cosa-1/2*sina)

=4*(3/4*cos^2a-1/4*sin^2a)

=3cos^2a-sin^2a

=3(1-sin^2a)-sin^2a

=3-4sin^2a

=>m=3; n=-4

m^2-n^2=-7

Ta có:

\(\dfrac{1}{cos^2x-sin^2x}+\dfrac{2tanx}{1-tan^2x}=\dfrac{1}{cos2x}+tan2x=\dfrac{1}{cos2x}+\dfrac{sin2x}{cos2x}=\dfrac{1+sin2x}{cos2x}=\dfrac{cos2x}{1-sin2x}\)

\(\Rightarrow P=a+b=2+1=3\)

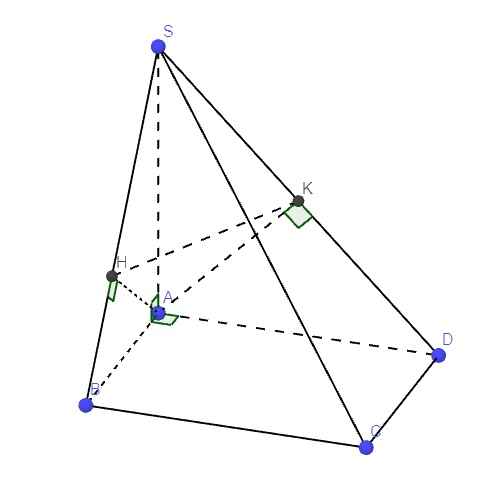
\(SA\perp\left(ABCD\right)\Rightarrow\left\{{}\begin{matrix}SA\perp AB\\SA\perp AD\end{matrix}\right.\) \(\Rightarrow\) các tam giác SAB và SAD vuông tại A

\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\BC\perp AB\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp SB\)

\(\Rightarrow\Delta SBC\) vuông tại B

\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\Rightarrow CD\perp SD\)

\(\Rightarrow\Delta SCD\) vuông tại D

b.

\(\left\{{}\begin{matrix}BC\perp\left(SAB\right)\Rightarrow BC\perp AH\\AH\perp SB\end{matrix}\right.\) \(\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH\perp SC\) (1)

\(\left\{{}\begin{matrix}CD\perp\left(SAD\right)\Rightarrow CD\perp AK\\AK\perp SD\end{matrix}\right.\) \(\Rightarrow AK\perp\left(SCD\right)\Rightarrow AK\perp SC\) (2)

(1);(2) \(\Rightarrow SC\perp\left(AHK\right)\)

2.B

3.C

4.A

a.

\(\lim\limits_{x\rightarrow2}\dfrac{x\sqrt{2x}+\sqrt{2x}-6}{x^2+2x-8}=\lim\limits_{x\rightarrow2}\dfrac{\left(x\sqrt{2x}-4\right)+\left(\sqrt{2x}-2\right)}{\left(x-2\right)\left(x+4\right)}\)

\(=\lim\limits_{x\rightarrow2}\dfrac{\dfrac{2x^3-16}{x\sqrt{2x}+4}+\dfrac{2x-4}{\sqrt{2x}+2}}{\left(x-2\right)\left(x+4\right)}\)

\(=\lim\limits_{x\rightarrow2}\dfrac{\dfrac{2\left(x-2\right)\left(x^2+2x+4\right)}{x\sqrt{2x}+4}+\dfrac{2\left(x-2\right)}{\sqrt{2x}+2}}{\left(x-2\right)\left(x+4\right)}\)

\(=\lim\limits_{x\rightarrow2}\dfrac{\dfrac{2\left(x^2+2x+4\right)}{x\sqrt{2x}+4}+\dfrac{2}{\sqrt{2x}+2}}{x+4}\)

\(=\dfrac{\dfrac{2\left(2^2+2.2+4\right)}{2\sqrt{4}+4}+\dfrac{2}{\sqrt{4}+2}}{2+4}\)

\(=...\)

b.

\(\lim\limits_{x\rightarrow-\infty}\dfrac{\sqrt{9x^2-3x+2}-3}{x+2}=\lim\limits_{x\rightarrow-\infty}\dfrac{\left|x\right|\sqrt{9-\dfrac{3}{x}+\dfrac{2}{x^2}}-3}{x+2}\)

\(=\lim\limits_{x\rightarrow-\infty}\dfrac{-x\sqrt{9-\dfrac{3}{x}+\dfrac{2}{x^2}}-3}{x+2}\)

\(=\lim\limits_{x\rightarrow-\infty}\dfrac{x\left(-\sqrt{9-\dfrac{3}{x}+\dfrac{2}{x^2}}-\dfrac{3}{x}\right)}{x\left(1+\dfrac{2}{x}\right)}\)

\(=\lim\limits_{x\rightarrow-\infty}\dfrac{-\sqrt{9-\dfrac{3}{x}+\dfrac{2}{x^2}}-\dfrac{3}{x}}{1+\dfrac{2}{x}}\)

\(=\dfrac{-\sqrt{9-0+0}-0}{1+0}=...\)

Huhuuuu giup e vs

a.

Do chóp tứ giác đều \(\Rightarrow\Delta SAC\) cân tại A

Mà O là tâm đáy \(\Rightarrow O\) là trung điểm AC

\(\Rightarrow SO\perp AC\) (trung tuyến đồng thời là đường cao trong tam giác cân)

Hoàn toàn tương tự, ta có \(SO\perp BD\)

\(\Rightarrow SO\perp\left(ABCD\right)\)

b.

Ta có: \(AC\perp BD\) (hai đường chéo hình vuông)

Theo cmt, \(SO\perp AC\)

\(\left\{{}\begin{matrix}SO\in\left(SBD\right)\\BD\in\left(SBD\right)\end{matrix}\right.\) \(\Rightarrow AC\perp\left(SBD\right)\)

Tương tự: \(\left\{{}\begin{matrix}BD\perp AC\\BD\perp SO\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)

14:

sin 2a=(sina+cosa)^2-1

=m^2-1

23:

 u4=10 và u7=22

=>\(\left\{{}\begin{matrix}u1+3d=10\\u1+6d=22\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3d=-12\\u1+3d=10\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}d=4\\u1=10-12=-2\end{matrix}\right.\)

=>Chọn C

Câu 22:

\(\left\{{}\begin{matrix}u1+2u5=0\\S_4=14\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}u1+2\left(u1+4d\right)=0\\4\cdot\dfrac{\left[2u1+3d\right]}{2}=14\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}3u1+8d=0\\2u1+3d=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6u1+16d=0\\6u1+9d=21\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}7d=-21\\2u_1+3d=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}d=-3\\2u_1=7-3d=7+9=16\end{matrix}\right.\)

=>\(u_1=8;d=-3\)

=>Chọn A

21A

19B