K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
26 tháng 10 2021
Câu 3:
b, PT hoành độ giao điểm (d1) và (d2) là
\(2x+1=\dfrac{1}{3}x\Leftrightarrow\dfrac{5}{3}x=-1\Leftrightarrow x=-\dfrac{3}{5}\Leftrightarrow y=-\dfrac{3}{5}\cdot\dfrac{1}{3}=-\dfrac{1}{5}\\ \Leftrightarrow A\left(-\dfrac{3}{5};-\dfrac{1}{5}\right)\)
Vậy \(A\left(-\dfrac{3}{5};-\dfrac{1}{5}\right)\) là giao điểm của 2 đths
Bài 5:
Gọi chân đường cao từ A đến BC là H
Ta có \(OA=CH=1,1\left(m\right);AH=1,6\left(m\right)\)
Áp dụng HTL: \(BH=\dfrac{AH^2}{CH}=\dfrac{128}{55}\left(m\right)\)
Do đó chiều cao tường là \(BC=BH+HC=\dfrac{377}{110}\approx3,4\left(m\right)\)
HA
0
11 tháng 3 2022
\(\Delta'=4-\left(m-1\right)=5-m\)
để pt có nghiệm kép khi \(5-m=0\Leftrightarrow m=5\)
chọn B
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 3 2022
Phương trình có nghiệm kép khi:
\(\Delta'=4-\left(m-1\right)=0\Leftrightarrow5-m=0\)
\(\Rightarrow m=5\)
T
1
2 tháng 1 2022
a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OM⊥AB
TL
1
2 tháng 9 2021
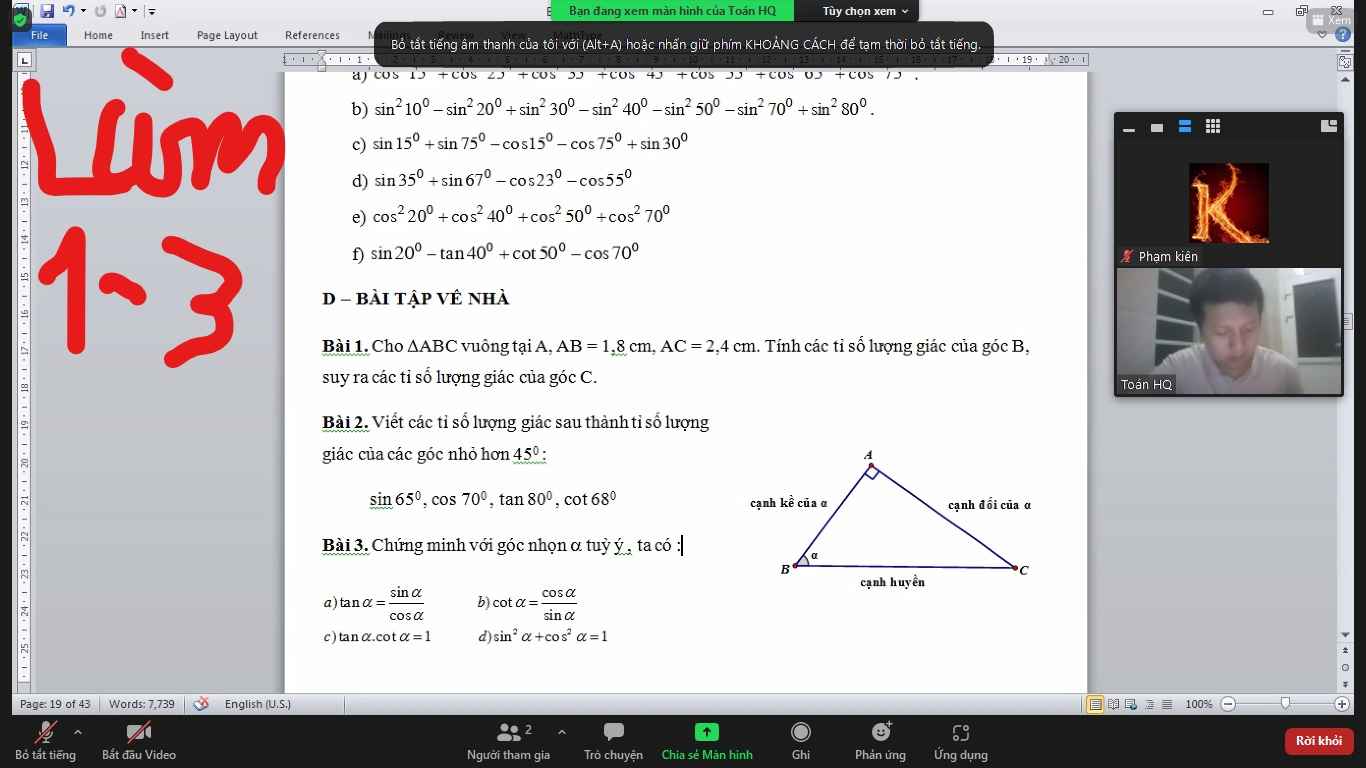
sin 650=cos 350
\(cos70^0=sin30^0\)
\(tan80^0=cot20^0\)
\(cot68^0=tan32^0\)
4 tháng 7 2021
a) Ta có: \(P=\left(\dfrac{\sqrt{a}+1}{\sqrt{ab}+1}+\dfrac{\sqrt{ab}+\sqrt{a}}{\sqrt{ab}-1}-1\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{ab}+1}-\dfrac{\sqrt{ab}+\sqrt{a}}{\sqrt{ab}-1}+1\right)\)
\(=\dfrac{\left(\sqrt{a}+1\right)\left(\sqrt{ab}-1\right)+\left(\sqrt{ab}+\sqrt{a}\right)\left(\sqrt{ab}+1\right)-\left(ab-1\right)}{\left(\sqrt{ab}+1\right)\left(\sqrt{ab}-1\right)}:\dfrac{\left(\sqrt{a}+1\right)\left(\sqrt{ab}-1\right)-\left(\sqrt{ab}+\sqrt{a}\right)\left(\sqrt{ab}+1\right)+ab-1}{\left(\sqrt{ab}+1\right)\left(\sqrt{ab}-1\right)}\)
\(=\dfrac{a\sqrt{b}-\sqrt{a}+\sqrt{ab}-1+ab+\sqrt{ab}+a\sqrt{b}+\sqrt{a}-ab+1}{\left(\sqrt{ab}+1\right)\left(\sqrt{ab}-1\right)}:\dfrac{a\sqrt{b}-\sqrt{a}+\sqrt{ab}-1-ab-\sqrt{ab}-a\sqrt{b}-\sqrt{a}+ab-1}{\left(\sqrt{ab}+1\right)\left(\sqrt{ab}-1\right)}\)
\(=\dfrac{2a\sqrt{b}+2\sqrt{ab}}{\left(\sqrt{ab}+1\right)\left(\sqrt{ab}-1\right)}\cdot\dfrac{\left(\sqrt{ab}+1\right)\left(\sqrt{ab}-1\right)}{-2\sqrt{a}-2}\)
\(=\dfrac{2\sqrt{ab}\left(\sqrt{a}+1\right)}{-2\left(\sqrt{a}+1\right)}\)
\(=-\sqrt{ab}\)
b) Ta có: \(b=\dfrac{\sqrt{3}-1}{\sqrt{3}+1}\)
\(=\dfrac{\left(\sqrt{3}-1\right)^2}{2}\)
\(=\dfrac{4-2\sqrt{3}}{2}=2-\sqrt{3}\)
Thay \(a=2+\sqrt{3}\) và \(b=2-\sqrt{3}\) vào P, ta được:
\(P=-\sqrt{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}=-1\)
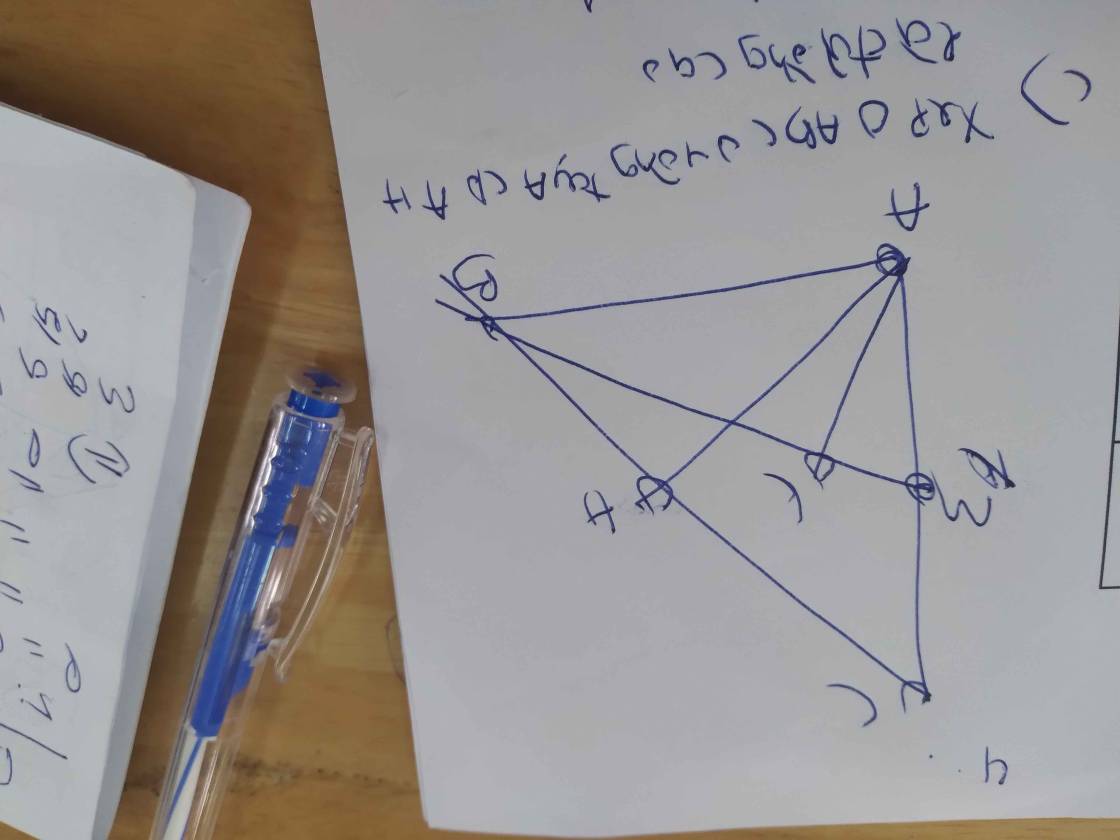
Bài 5:
Gọi giá tiền mỗi chiếc áo bạn Hoa đã mua là x(nghìn đồng)
(Điều kiện: x>0)
Giá tiền ban đầu của mỗi chiếc áo là x+30(nghìn đồng)
Số lượng áo dự định là \(\dfrac{600}{x+30}\)(cái)
Số lượng áo thực tế là \(\dfrac{600}{x}\)(cái)
Vì số lượng áo thực tế mua được bằng 1,25 lần số lượng áo ban đầu định mua thì \(\dfrac{600}{x}=1,25\cdot\dfrac{600}{x+30}\)
=>\(\dfrac{600}{x}=\dfrac{750}{x+30}\)
=>\(\dfrac{4}{x}=\dfrac{5}{x+30}\)
=>5x=4x+120
=>x=120(nhận)
Vậy: Giá tiền của mỗi chiếc áo thực tế là 120 nghìn đồng