Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.
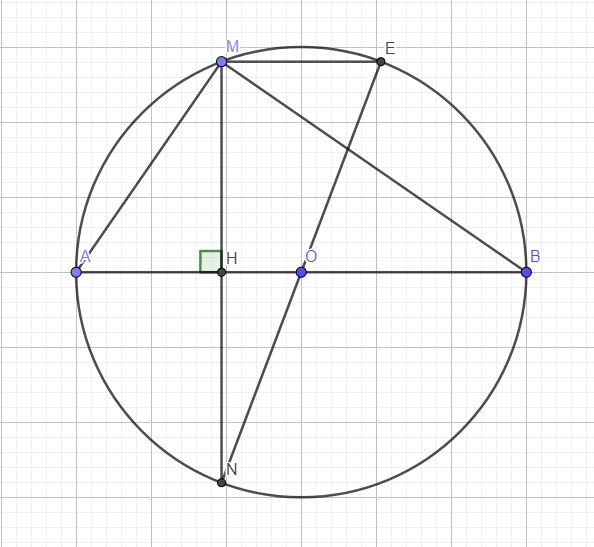
Do \(ME||AB\Rightarrow\stackrel\frown{AM}=\stackrel\frown{EB}\) (hai dây song song chắn hai cung bằng nhau) (1)
Gọi H là giao điểm MN và AB
\(\Rightarrow H\) là trung điểm AB (đường kính vuông góc dây cung)
Trong tam giác AMN, AH vừa là đường cao vừa là trung tuyến
\(\Rightarrow\Delta AMN\) cân tại A \(\Rightarrow AM=AN\)
\(\Rightarrow\stackrel\frown{AM}=\stackrel\frown{AN}\) (2)
(1);(2) \(\Rightarrow\stackrel\frown{AM}=\stackrel\frown{AN}=\stackrel\frown{EB}\)
b.
Do \(\left\{{}\begin{matrix}ME||AB\\MN\perp AB\end{matrix}\right.\) \(\Rightarrow ME\perp MN\)
\(\Rightarrow\widehat{NME}=90^0\)
\(\Rightarrow\widehat{NME}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow NE\) là đường kính
\(\Rightarrow\) 3 điểm N, O, E thẳng hàng

Đáp án D
Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy
\(sin\widehat{MAE}=\dfrac{ME}{AM}=\dfrac{1}{2}\Rightarrow\widehat{MAE}=30^0\)
AB qua trung điểm của dây \(\Rightarrow sđ\stackrel\frown{BM}=sđ\stackrel\frown{BN}\Rightarrow\widehat{BAN}=\widehat{MAE}=30^0\)
\(\Rightarrow\widehat{BMN}=\widehat{BAN}=30^0\) (cùng chắn BN)