
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)Đk:\(x\ne4\)
\(\dfrac{x^4}{4-x}+x^3+1=\dfrac{x^4+\left(x^3+1\right)\left(4-x\right)}{4-x}\)\(=\dfrac{x^4+\left(-x^4+4x^3+4-x\right)}{4-x}=\dfrac{4x^3-x+4}{4-x}\)
b) Đk: \(x\ne0;x\ne1\)
\(\dfrac{1}{x^2-x}+\dfrac{2x}{x-1}=\dfrac{1}{x\left(x-1\right)}+\dfrac{2x^2}{x\left(x-1\right)}=\dfrac{1+2x^2}{x\left(x-1\right)}\)


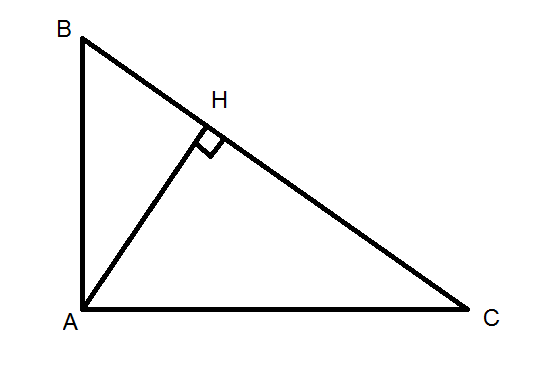
a. △ABH và △CBA có: \(\widehat{B}\) chung; \(\widehat{AHB}=\widehat{CAB}=90^0\).
\(\Rightarrow\)△ABH∼△CBA (g-g).
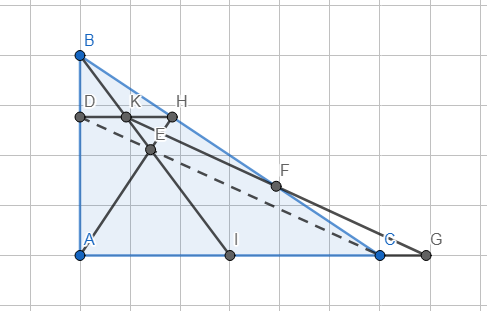
b. △ABI có: DK//AI (cùng vuông góc AB).
\(\Rightarrow\dfrac{DK}{AI}=\dfrac{BK}{BI}\)
△CBI có: KH//CI (cùng vuông góc AB).
\(\Rightarrow\dfrac{HK}{CI}=\dfrac{BK}{BI}=\dfrac{DK}{AI}\Rightarrow HK=DK\Rightarrow\)K là trung điểm DH.
c. Qua K kẻ đg thẳng song song DC cắt BC, AC tại F,G.
△HDC có: KF//DC, K là trung điểm DH \(\Rightarrow\)F là trung điểm HC.
\(\Rightarrow\)△KHF=△GCF (g-c-g) \(\Rightarrow KH=CG\).
△KHE có: KH//AI \(\Rightarrow\dfrac{KE}{EI}=\dfrac{KH}{AI}=\dfrac{CG}{CI}\Rightarrow\)EC//KG
\(\Rightarrow\)D,C,E thẳng hàng.

-Gọi x (đồng) là giá niêm yết của chai nước rửa tay sát khuẩn (x>0).
a là số chai nước rửa tay nhiều nhất có thể mua đc sau khi khuyến mãi
(a là số tự nhiên khác 0).
-Số tiền An mang theo là: \(9x\left(đồng\right)\)
-Giá tiền của chai nước rửa tay sát khuẩn sau khi khuyến mãi là:
\(\left[x.\left(100\%-20\%\right)\right]=\dfrac{4}{5}x\left(đồng\right)\)
-Từ đề bài ta có BĐT sau:
\(9x\ge x+a.\dfrac{4}{5}x\).
\(\Leftrightarrow9x-x-a.\dfrac{4}{5}x\ge0\)
\(\Leftrightarrow\left(8-\dfrac{4}{5}a\right)x\ge0\)
Vì \(x>0\) nên BĐT đã cho tương đương:
\(8-\dfrac{4}{5}a\ge0\)
\(\Leftrightarrow a\le10\).
Mà a là số chai nước rửa tay nhiều nhất có thể mua đc sau khi khuyến mãi.
\(\Rightarrow a=10\)
-Vậy bạn An có thể mua được 10 chai nước theo chương trình khuyến mãi trên.

a: Ta có: \(\left(x-3\right)^3-\left(x-3\right)\left(x^2+3x+9\right)+9\left(x+1\right)^2=4\)
\(\Leftrightarrow x^3-9x^2+27x-27-x^3+27+9x^2+18x+9=4\)
\(\Leftrightarrow45x=-5\)
hay \(x=-\dfrac{1}{9}\)
b: Ta có: \(x\left(x-5\right)\left(x+5\right)-\left(x+2\right)\left(x^2-2x+4\right)=17\)
\(\Leftrightarrow x^3-25x-x^3-8=17\)
\(\Leftrightarrow-25x=25\)
hay x=-1

a: Xét ΔHEB vuông tại E và ΔHDC vuông tại D có
\(\widehat{EHB}=\widehat{DHC}\)
Do đó: ΔHEB\(\sim\)ΔHDC
Suy ra: HE/HD=HB/HC
hay \(HE\cdot HC=HB\cdot HD\)
b: Xét ΔHED và ΔHBC có
HE/HB=HD/HC
\(\widehat{EHD}=\widehat{BHC}\)
Do đó: ΔHED\(\sim\)ΔHBC
Suy ra: \(\widehat{HED}=\widehat{HBC}\)

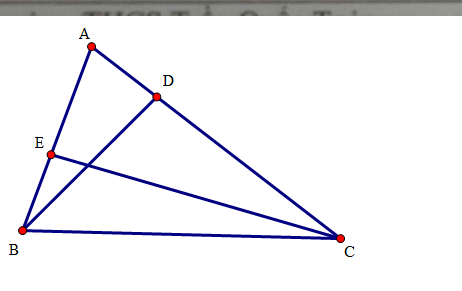
a: Xét ΔBED vuông tại E và ΔBAC vuông tại A có
góc B chung
=>ΔBED đồng dạng với ΔBAC
b: Xét ΔCAB có FD//AB
nên CD/DB=CF/FA
=>DB/DC=FA/FC








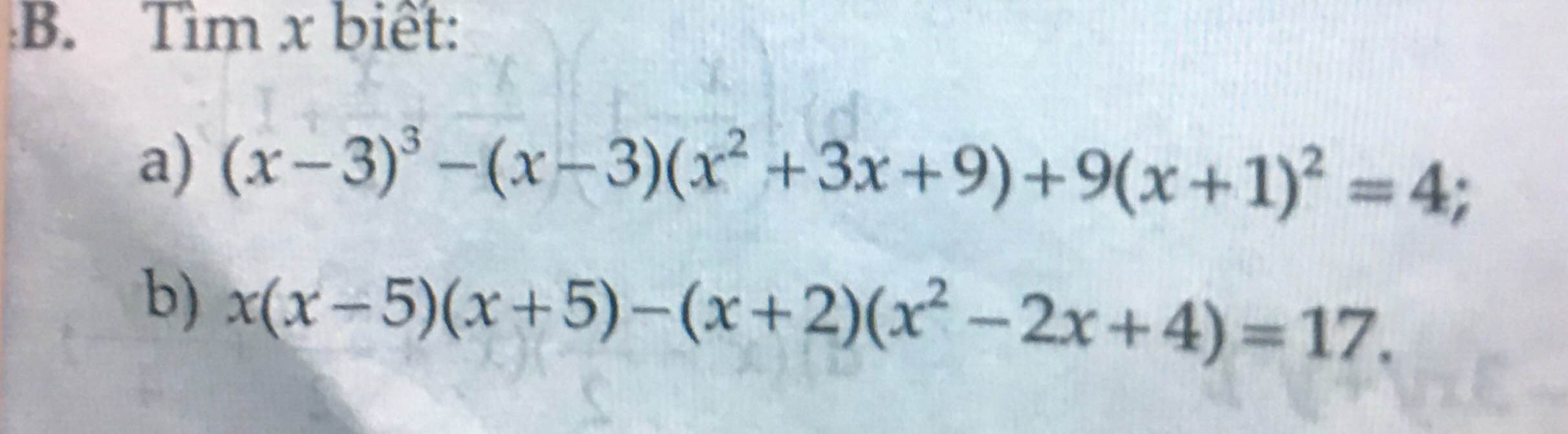



Câu 1:
a) \(3x\left(x-2\right)+5\left(x-2\right)=\left(3x+5\right)\left(x-2\right)\).
b) \(x^2-2x-9y^2-6y=\left(x^2-9y\right)-2\left(x+3y\right)=\left(x-3y\right)\left(x+3y\right)-2\left(x+3y\right)=\left(x-3y-2\right)\left(x+3y\right)\)c) \(x^4+x^3+2x^2+x+1=\left(x^4+x^3+x^2\right)+\left(x^2+x+1\right)=\left(x^2+1\right)\left(x^2+x+1\right)\).
Câu 1 :
a, \(3x\left(x-2\right)+5\left(x-2\right)=\left(3x+5\right)\left(x-2\right)\)
b, \(x^2-2x-9y^2-6y=\left(x^2-9y^2\right)+\left(-2x-6y\right)\)
\(=\left(x-3y\right)\left(x+3y\right)-2\left(x+3y\right)=\left(x-3y-2\right)\left(x+3y\right)\)
c, \(x^4+x^3+2x^2+x+1=\left(x^4+2x^2+1\right)+\left(x^3+x\right)\)
\(=\left(x^2+1\right)+x\left(x^2+1\right)=\left(x+1\right)\left(x^2+1\right)\)
nhẹ ngàng tình cảm :>>