
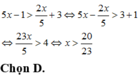
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

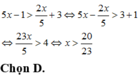

Do hai vế của phương trình đều dương nên lấy logarit cơ số 3 hai vế ta được :
![]()
![]()
![]()
![]()
Chọn D

Do hai vế của phương trình đều dương nên lấy logarit cơ số 3 hai vế ta được :
![]()
![]()
![]()
![]()
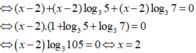
Chọn D

Đáp án A.
+ Điều kiện: x > 0
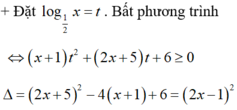
Bất phương trình
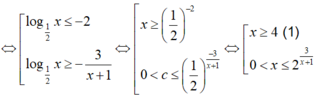
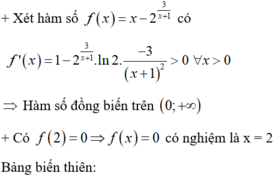
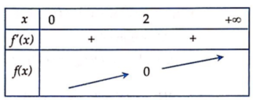
=> Bất phương trình x ≤ 2 3 x + 1 ⇔ f ( x ) ≤ 0 ⇔ 0 < x ≤ 2 ( 2 ) .
Từ (1) và (2) => Tập nghiệm của bất phương trình là
S = ( 0 ; 2 ] ∪ [ 4 ; + ∞ ) .
Vậy có 2016 nghiệm nguyên thỏa mãn.

Đáp án C
Vì x = 1 là một nghiệm của bất phương trình
![]()
Khi đó, bất phương trình
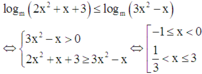

Điều kiện: 1≤ x≤ 3
Với điều kiện trên bpt
( x - 1 ) 2 + 2 + x - 1 > ( 3 - x ) 2 + 2 + 3 - x
Xét f ( t ) = t 2 + 2 + t v ớ i t ≥ 0
có f ' ( t ) = 1 2 t 2 + 2 + 1 2 t > 0 ∀ t > 0
Do đó hàm số đồng biến trên [0; +∞).
Khi đó (1) tương đương f(x-1) > f(3-x) hay x-1> 3-x
Suy ra x > 2
So với điều kiện, bpt có tập nghiệm là (2; 3] và 4a- b= 5
Chọn C.