Đáp án C

Cách giải:

Xét các số x = a; y = b + 1; z = c + 2; t = d + 3. Vì 1 ≤ a ≤ b ≤ c ≤ d ≤ 9 => 1 ≤ x < y < z < t ≤ 12 (*)

Và mỗi bộ 4 số (x;y;z;t) được chọn từ tập hợp 1 ; 2 ; . . . . ; 12  ta đều thu được bộ số thỏa mãn  (*). Do đó, số cách chọn 4 số trong 12 số là C 12 4   =   495  số suy ra  n ( X )   =   495

Số phần tử của không gian mẫu là   n ( Ω )   =   9 . 10 . 10 . 10 = 9000

Vậy xác suất cần tính là

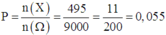
Chọn D

Chọn số tự nhiên có 4 chữ số bất kỳ có: (cách).

Gọi A là biến cố: “Số được chọn có dạng  a b c d ¯ , trong đó 1 ≤ a ≤ b ≤ c ≤ d ≤ 9” . (*)

Cách 1: Dùng tổ hợp

Nhận xét rằng với 2 số tự nhiên bất kỳ ta có: 

Do đó nếu đặt:

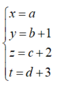
Từ giả thuyết  ta suy ra: 

Với mỗi tập con gồm 4 phần tử đôi một khác nhau được lấy ra từ {1,2,....,12}ta đều có được duy nhất một bộ số thoả mãn (**) và do đó tương ứng ta có duy nhất một bộ số (a,b,c,d) thoả mãn (*). Số cách chọn tập con thoả tính chất trên là tổ hợp chập 4 của 12 phần tử, do đó: 

Vậy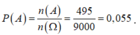 

Cách 2: Dùng tổ hợp lặp

Chọn số tự nhiên có 4 chữ số bất kỳ có: (cách).

Mỗi tập con có 4 phần tử được lấy từ tập {1,2,...,9}(trong đó mỗi phần tử có thể được chọn lặp lại nhiều lần) ta xác định được một thứ tự không giảm duy nhất và theo thứ tự đó ta có được một số tự nhiên có dạng   a b c d ¯ (trong đó ). Số tập con thoả tính chất trên là số tổ hợp lặp chập 4 của 9 phần tử

Do đó theo công thức tổ hợp lặp ta có:

 Vậy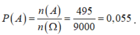 

Không gian mẫu: \(C_9^3\)

Có 2 cách lấy thỏa mãn: (2 quả số 1, một quả số 3) hoặc (1 quả số 1, hai quả số 2)

\(\Rightarrow C_2^2.C_4^1+C_2^1.C_3^2\) cách

Xác suất: \(P=\dfrac{C_2^2.C_4^1+C_2^1.C_3^2}{C_9^3}=...\)

Gọi A là xác suất lấy được 3 sản phẩm tốt.

\(\Rightarrow P\left(A\right)=\dfrac{C^3_6.C^1_6}{C^4_{12}}=\dfrac{8}{33}\)

Đáp án A

Số cách chọn ngẫu nhiên 2 giáo viên từ 30 giáo viên là: 

Số cách chọn ngẫu nhiên 2 giáo viên khác trường là:  

Xác suất chọn 2 giáo viên khác trường là: 

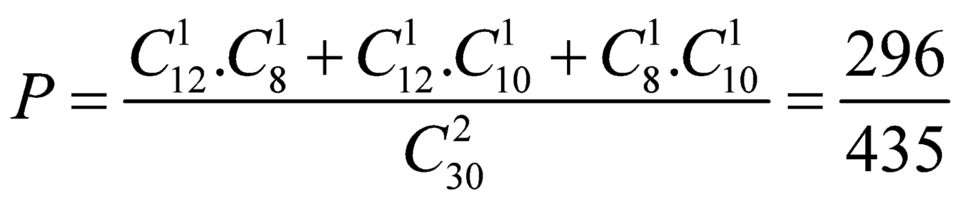
a. Không gian mẫu: \(C_{10}^3\)

Số cách chọn 3 số nguyên liên tiếp: 8 cách (123; 234;...;8910)

Số cách chọn ra 3 số trong đó có đúng 2 số nguyên liên tiếp:

- Cặp liên tiếp là 12 hoặc 910 (2 cách): số còn lại có 7 cách chọn

- Cặp liên tiếp là 1 trong 7 cặp còn lại: số còn lại có 6 cách chọn

Vậy có: \(C_{10}^3-\left(8+2.7+7.6\right)=56\) bộ thỏa mãn

Xác suất: \(P=\dfrac{56}{C_{10}^3}=...\)

b.

Có 2 số chia hết cho 4 là 4 và 8

Rút ra k thẻ: \(C_{10}^k\) cách

Số cách để trong k thẻ có ít nhất 1 thẻ chia hết cho 4: \(C_{10}^k-C_8^k\)

Xác suất thỏa mãn: \(P=\dfrac{C_{10}^k-C_8^k}{C_{10}^k}>\dfrac{13}{15}\)

\(\Leftrightarrow\dfrac{2}{15}>\dfrac{C_8^k}{C_{10}^k}=\dfrac{\dfrac{8!}{k!\left(8-k\right)!}}{\dfrac{10!}{k!\left(10-k\right)!}}=\dfrac{\left(9-k\right)\left(10-k\right)}{90}\)

\(\Leftrightarrow\left(9-k\right)\left(10-k\right)-12< 0\Leftrightarrow k^2-19k+78< 0\)

\(\Rightarrow6< k< 13\)