Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
S = ∫ 0 π cos x d x = ∫ 0 π / 2 cos x d x − ∫ π / 2 π cos x d x = sin x 0 π / 2 − sin x π / 2 π = 1 − 0 − 1 = 2.
Theo giả thiết và công thức tích phân từng phần, ta có:
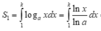
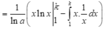
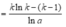
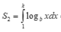
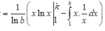
Vậy 
Chọn đáp án A.
Đáp án D
y ' = 4 a x 3 + 2 b x , y ' 1 = - 4 a - 2 b
Phương trình tiếp tuyến tại A là: d: y=(-4a-2b)(x+1)
Xét phương trình tương giao: a x 4 + b x 2 + c = ( - 4 a - 2 b ) ( x + 1 )
Phương trình có 2 nghiệm x=0,x=2 => 4 a + 2 b + c = 0 28 a + 10 b + c = 0 ( 1 )
∫ 0 2 - 4 a - 2 b x + 1 - a x 4 - b x 2 - c d x = - 2 a - b x 2 + - 4 a - 2 b x - a x 5 5 - b x 3 3 - c x 2 0 = - 112 5 a - 32 3 b - 2 c = 28 5 2 1 , 2 ⇒ a = 1 b = - 3 ⇒ y = x 4 - 3 x 2 + 2 , d : y = 2 x + 2 c = 2 ⇒ S = ∫ - 1 0 x 4 - 3 x 2 + 2 d x = x 5 5 - x 3 - x 2 0 - 1 = 1 5
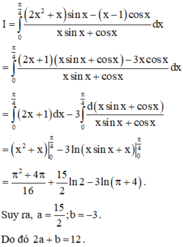
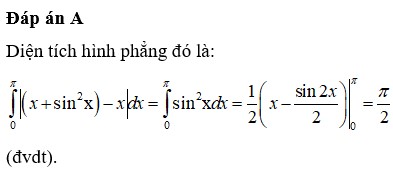
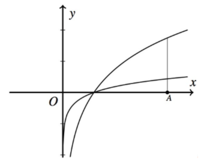
Đáp án B
Phương pháp: Sử dụng công thức ứng dụng của tích phân để tính diện tích hình phẳng.
Cách giải: Xét phương trình hoành độ giao điểm
sinx = cosx <=> tanx = 1 <=> x = π 4 + k π
TH1: a = π 4 =>
=> không thỏa mãn
TH2: a = π 2 =>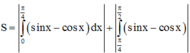
=> không thỏa mãn
TH3: a ∈ π 4 ; π 2
=>
=>
<=>
<=>
<=>
=>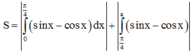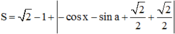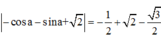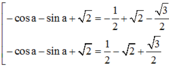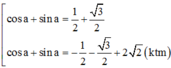