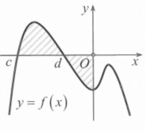
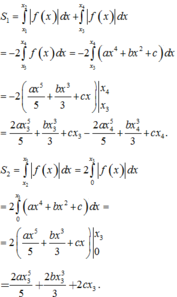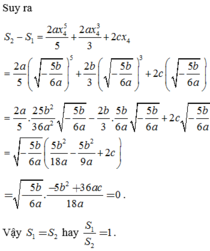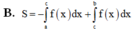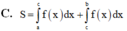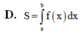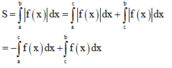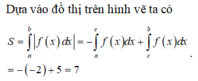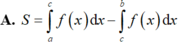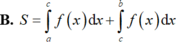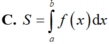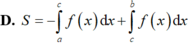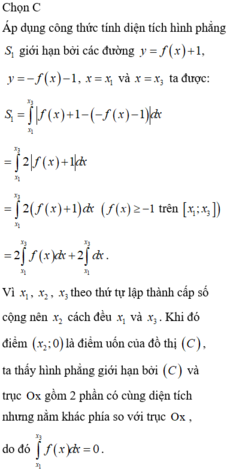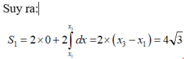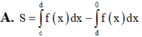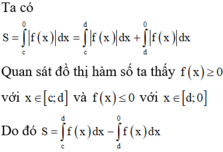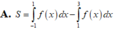Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương trình hoành độ giao điểm của đồ thị f ( x ) và Ox: a x 4 + b x 2 + c = 0 .
Để phương trình có bốn nghiệm
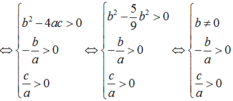
Gọi x 1 , x 2 , x 3 , x 4 lần lượt là bốn nghiệm của phương trình a x 4 + b x 2 + c = 0 và x 1 < x 2 < x 3 < x 4 . Không mất tính tổng quát, giả sử a > 0 .
Khi đó
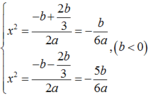
Suy ra x 1 = - - 5 b 6 a ; x 2 = - - b 6 a ; x 3 = - b 6 a ; x 4 = - b 6 a .
Do đồ thị hàm số f ( x ) nhận trục tung làm trục đối xứng nên ta có:
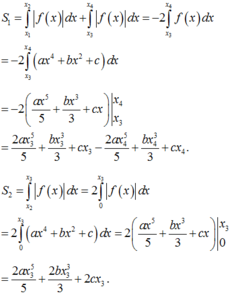
Suy ra
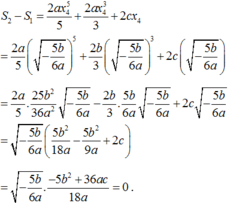
Vậy S 1 = S 2 hay S 1 S 2 = 1 .

Đáp án A
Phương pháp
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành, x = a; x = b là S = ∫ a b f x d x
Cách giải:
Xét phương trình hoành độ giao điểm của đồ thị y = x 4 + x 2 với trục hoành là x 4 + x 2 = 0 ⇔ x = 0
Diện tích hình phẳng cần tìm là
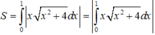
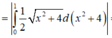
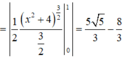
Suy ra
![]()

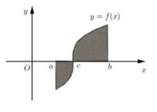
Chọn D
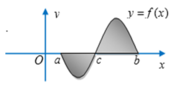
Ta có
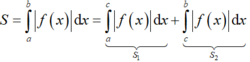
Vì f(x) < 0, ∀ x ∈ a ; c nên |f(x)| = –f(x).
Do đó, S 1 = - ∫ a c f x d x .
Tương tự, f(x) > 0, ∀ x ∈ a ; c nên |f(x)| = f(x).
Do đó, S 2 = ∫ c b f x d x .
Vậy S = - ∫ a c f x d x + ∫ c b f x d x .

Chọn: B
Phương trình hoành độ giao điểm của
đồ thị hàm số y=f(x) và trục hoành:
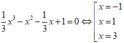
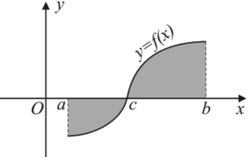
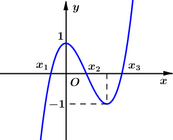
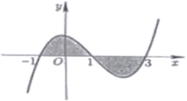
Từ hình vẽ ta thấy
![]()
Do đó
![]()
Suy ra các phương án A, C, D đúng.