Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Cách 1: Tư duy tự luận
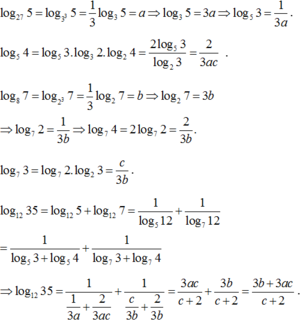
Cách 2: Sử dụng máy tính cầm tay
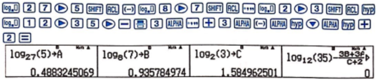

Bài 1:
\(A=\log_380=\log_3(2^4.5)=\log_3(2^4)+\log_3(5)\)
\(=4\log_32+\log_35=4a+b\)
\(B=\log_3(37,5)=\log_3(2^{-1}.75)=\log_3(2^{-1}.3.5^2)\)
\(=\log_3(2^{-1})+\log_33+\log_3(5^2)=-\log_32+1+2\log_35\)
\(=-a+1+2b\)
Bài 2:
\(\log_{30}8=\frac{\log 8}{\log 30}=\frac{\log (2^3)}{\log (10.3)}=\frac{3\log2}{\log 10+\log 3}\)
\(=\frac{3\log (\frac{10}{5})}{1+\log 3}=\frac{3(\log 10-\log 5)}{1+\log 3}=\frac{3(1-b)}{1+a}\)

a) Ta có:
a = log 3 15 = log 3 ( 3 , 5 ) = log 3 3 + log 3 5 = 1 + log 3 5
Suy ra log 3 5 = a – 1
b = log 3 10 = log 3 ( 2 , 5 ) = log 3 2 + log 3 5
Suy ra log 3 2 = b − log 3 5 = b − (a − 1) = b – a + 1
Do đó:
log 3 50 = log 3 0 , 5 ( 2 . 52 ) = 2 log 3 2 + 4 log 3 5 = 2 (b – a + 1) + 4(a − 1) = 2a + 2b − 2
b) Ta có:
log 140 63 = log 140 ( 32 . 7 ) = 2 log 140 3 + log 140 7
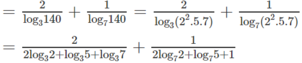
Từ đề bài suy ra:
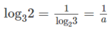
log 0 , 5 π . log 7 5 = log 7 2 . log 2 3 . log 35 = cab
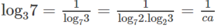
Vậy
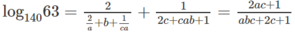

Ta có:
log 140 63 = log 140 3 2 . 7 = 2 log 140 3 + log 140 7
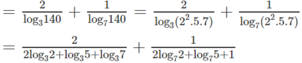
Từ đề bài suy ra:
![]()
loh 0 , 5 π . log 7 5 = log 7 2 . log 2 3 . log 35 = cab
![]()
Vậy
![]()

5.
Gọi M là trung điểm BC \(\Rightarrow AM\perp BC\)
\(\Rightarrow BC\perp\left(A'AM\right)\)
\(\Rightarrow\widehat{A'MA}\) là góc giữa (A'BC) và (ABC)
\(\Rightarrow\widehat{A'MA}=60^0\)
\(AM=\frac{a\sqrt{3}}{2}\Rightarrow A'A=AM.tan60^0=\frac{3a}{2}\)
\(B=\frac{a^2\sqrt{3}}{4}\Rightarrow V=B.A'A=\frac{3\sqrt{3}}{8}a^3\)
1.
\(V=Bh\)
2.
\(B=\frac{a^2\sqrt{3}}{4}\Rightarrow V=Bh=\frac{a^2\sqrt{3}}{4}.a\sqrt{6}=\frac{3\sqrt{2}}{4}a^3\)
3.
\(B=\frac{1}{2}\left(a\sqrt{2}\right)^2=a^2\Rightarrow V=Bh=a^2.5a=5a^3\)
4.
\(h=\sqrt{\left(2a\right)^2-\left(a\sqrt{3}\right)^2}=a\)
\(B=\frac{\left(a\sqrt{3}\right)^2\sqrt{3}}{4}=\frac{3\sqrt{3}}{4}a^2\)
\(V=Bh=\frac{3\sqrt{3}}{4}a^3\)
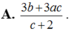
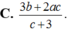
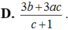


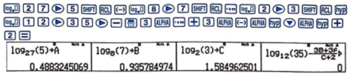
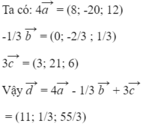
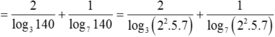
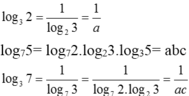
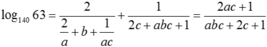
Chọn A.
Ta có:
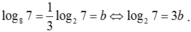
Mà