Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
\(y'=x^2-2mx+m^2-4\)
\(y''=2x-2m,\forall x\in R\)
Để hàm số \(y=\dfrac{1}{3}x^3-mx^2+\left(m^2-4\right)x+3\) đạt cực đại tại x = 3 thì:
\(\left\{{}\begin{matrix}y'\left(3\right)=0\\y''\left(3\right)< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2-6m+5=0\\6-2m< 0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m=1,m=5\\m>3\end{matrix}\right.\Leftrightarrow m=5\)
=> B.

a) 
f′(x) > 0 trên khoảng (-4; 0) và f’(x) < 0 trên khoảng (0; 4).
Hàm số đạt cực đại tại x = 0 và f C Đ = 5
Mặt khác, ta có f(-4) = f(4) = 3
Vậy 
d) f(x) = | x 2 − 3x + 2| trên đoạn [-10; 10]
Khảo sát sự biến thiên và vẽ đồ thị của hàm số g(x) = x 2 – 3x + 2.
Ta có:
g′(x) = 2x − 3; g′(x) = 0 ⇔ x = 3/2
Bảng biến thiên:

Vì

nên ta có đồ thị f(x) như sau:

Từ đồ thị suy ra: min f(x) = f(1) = f(2) = 0; max = f(x) = f(−10) = 132
e) 
f′(x) < 0 nên và f’(x) > 0 trên (π/2; 5π/6] nên hàm số đạt cực tiểu tại x = π/2 và f C T = f(π/2) = 1
Mặt khác, f(π/3) = 2√3, f(5π/6) = 2
Vậy min f(x) = 1; max f(x) = 2
g) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
f′(x) = 2cosx + 2cos2x = 4cos(x/2).cos3(x/2)
f′(x) = 0
⇔ 
Ta có: f(0) = 0,

Từ đó ta có: min f(x) = −2 ; max f(x) = 3√3/2

Bài 3:
Áp dụng các hằng đẳng thức đáng nhớ ta có:
$C=a^4+b^4=(a^2+b^2)^2-2a^2b^2$
$=[(a+b)^2-2ab]^2-2(ab)^2$
$=(8^2-2.15)^2-2.15^2=706$
Bài 2:
a)
$D=-x^2+6x-11=-11-(x^2-6x)=-2-(x^2-6x+9)$
$=-2-(x-3)^2$
Vì $(x-3)^2\geq 0$ với mọi $x$ nên $D=-2-(x-3)^2\leq -2$
Vậy GTLN của $D$ là $-2$ khi $(x-3)^2=0\Leftrightarrow x=3$
b)
$F=4x-x^2+1=1-(x^2-4x)=5-(x^2-4x+4)=5-(x-2)^2$
$\leq 5-0=5$
Vậy $F_{\max}=5$. Giá trị này được khi $(x-2)^2=0\leftrightarrow x=2$

Do \(x;y\in\left[0;2\right]\Rightarrow\left\{{}\begin{matrix}x\left(2-x\right)\ge0\\y\left(2-y\right)\ge0\end{matrix}\right.\) \(\Rightarrow2x^2+4y^2\le4x+8y\)
\(P\le3^0+5^0+3^z+4\left(x+2y\right)=2+3^z+4\left(6-z\right)=3^z-4z+26\)
Xét hàm \(f\left(z\right)=3^z-4z+26\) trên \(\left[0;2\right]\)
\(f'\left(z\right)=3^z.ln3-4=0\Rightarrow z=log_3\left(\dfrac{4}{ln3}\right)=a\)
\(f\left(0\right)=27\) ; \(f\left(2\right)=27\); \(f\left(a\right)\approx-1,1\)
\(\Rightarrow f\left(z\right)\le27\Rightarrow maxP=27\)
(Dấu "=" xảy ra khi \(\left(x;y;z\right)=\left(0;2;2\right)\))
Ồ mà khoan, bài trước bị nhầm lẫn ở chỗ \(3^{2x-x^2}+5^{2y-y^2}\ge3^0+5^0\) mới đúng, ko để ý bị ngược dấu đoạn này
Vậy giải cách khác:
\(0\le x;y;z\le2\Rightarrow x\left(2-x\right)\ge0\Rightarrow2x-x^2\ge0\)
Lại có: \(2x-x^2=1-\left(x-1\right)^2\le1\)
\(\Rightarrow0\le2x-x^2\le1\)
Tương tự ta có: \(0\le2y-y^2\le1\)
Xét hàm: \(f\left(t\right)=3^t-2t\) trên \(\left[0;1\right]\)
\(f'\left(t\right)=3^t.ln3-2=0\Rightarrow t=log_3\left(\dfrac{2}{ln3}\right)=a\)
\(f\left(0\right)=1;\) \(f\left(1\right)=1\) ; \(f\left(a\right)\approx0,73\)
\(\Rightarrow f\left(t\right)\le1\Rightarrow3^t-2t\le1\Rightarrow3^t\le2t+1\)
\(\Rightarrow3^{2x-x^2}\le2\left(2x-x^2\right)+1\)
Hoàn toàn tương tự, ta chứng minh được:
\(5^t\le4t+1\) với \(t\in\left[0;1\right]\Rightarrow5^{2y-y^2}\le4\left(2y-y^2\right)+1\)
\(3^t\le4t+1\) với \(t\in\left[0;2\right]\Rightarrow3^z\le4z+1\)
\(\Rightarrow P\le2\left(2x-x^2\right)+4\left(2y-y^2\right)+4z+3+2x^2+4y^2=4\left(x+2y+z\right)+3=27\)
Lần này thì ko sai được rồi

Lời giải:
\(a+b=3\Rightarrow a+(b-2)=1\Rightarrow b-2=1-a\)
Ta có:
\(f(x)=\frac{9^x}{9^x+3}\Rightarrow f(a)=\frac{9^a}{9^a+3}\) (1)
\(f(b-2)=f(1-a)=\frac{9^{1-a}}{9^{1-a}+3}=\frac{9}{9^a\left(\frac{9}{9^a}+3\right)}\)
\(=\frac{9}{9+3.9^a}=\frac{3}{3+9^a}\) (2)
Từ (1),(2) suy ra \(f(a)+f(b-2)=\frac{9^a}{9^a+3}+\frac{3}{3+9^a}=\frac{9^a+3}{9^a+3}=1\)
Đáp án A

\(y'=-3x^2+6mx+3\left(1-m^2\right)\)
Thực hiện phép chia \(y\) cho \(y'\) và lấy phần dư ta được phương trình đường thẳng đi qua 2 cực trị là: \(y=2x-m^2+m\)
Do \(A\in d\Rightarrow-2=2.2-m^2+m\Leftrightarrow-m^2+m+6=0\Rightarrow\left[{}\begin{matrix}m=3\\m=-2\end{matrix}\right.\)
Đáp án đúng là đáp án C
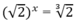
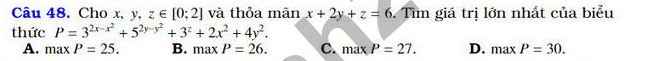
Chọn A