có ai chơi ff ko

(P) : y = ax2 + bx + c

Parabol có đỉnh I(1 ; 4) ⇒ –b/2a = 1 ⇒ b = –2a ⇒ 2a + b = 0.

Parabol đi qua I(1; 4) ⇒ 4 = a.12 + b . 1 + c ⇒ a + b + c = 4.

Paraol đi qua D(3; 0) ⇒ 0 = a.32 + b.3 + c ⇒ 9a + 3b + c = 0.

Giải hệ phương trình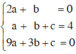  

ta được : a = –1 ; b = 2 ; c = 3.

Vậy a = –1 ; b = 2 ; c = 3.

a=-1,b=2,c=3

+ Parabol y = ax2 + bx + c đi qua điểm A (8; 0)

⇒ 0 = a.82 + b.8 + c ⇒ 64a + 8b + c = 0 (1).

+ Parabol y = ax2 + bx + c có đỉnh là I (6 ; –12) suy ra:

–b/2a = 6 ⇒ b = –12a (2).

–Δ/4a = –12 ⇒ Δ = 48a ⇒ b2 – 4ac = 48a (3) .

Thay (2) vào (1) ta có: 64a – 96a + c = 0 ⇒ c = 32a.

Thay b = –12a và c = 32a vào (3) ta được:

(–12a)2 – 4a.32a = 48a

⇒ 144a2 – 128a2 = 48a

⇒ 16a2 = 48a

⇒ a = 3 (vì a ≠ 0).

Từ a = 3 ⇒ b = –36 và c = 96.

Vậy a = 3; b = –36 và c = 96.

Cai nay la mon Sinh hoc dung khong?

ta có hệ sau :

\(\hept{\begin{cases}a.3^2+b.3-1=-7&-\frac{b}{2a}=1&\end{cases}\Leftrightarrow\hept{\begin{cases}9a+3b=-6\\b=-2a\end{cases}}\Leftrightarrow\hept{\begin{cases}a=-2\\b=4\end{cases}}}\)

vậy \(2a+b=0\)

Theo đề, ta có: c=4

Theo đề, ta có:

\(\left\{{}\begin{matrix}-\dfrac{b}{2a}=1\\-\dfrac{b^2}{16a}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\4a^2+80a=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-20\\b=40\end{matrix}\right.\)

\(\left\{{}\begin{matrix}-\dfrac{b}{2a}=2\\\dfrac{4ac-b^2}{4a}=-2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=-4a\\12a-16a^2=-8a\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}b=-4a\\a=\dfrac{5}{4}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{5}{4}\\b=-5\end{matrix}\right.\)

\(\Rightarrow a+2b=...\)

\(ĐK:a\ne0\)

\(A\left(0;1\right)\in\left(P\right)\Leftrightarrow c=1\)

(P) có đỉnh trên trục hoành \(\Leftrightarrow\Delta=b^2-4ac=0\Leftrightarrow b^2=4ac=4a\Leftrightarrow a=\dfrac{b^2}{4}\)

\(B\left(2;1\right)\in\left(P\right)\Leftrightarrow4a+2b+c=1\\ \Leftrightarrow b^2+2b=0\\ \Leftrightarrow\left[{}\begin{matrix}b=0\Leftrightarrow a=0\left(ktm\right)\\b=-2\Leftrightarrow a=1\left(tm\right)\end{matrix}\right.\)

Vậy \(a+b+c=1-2+1=0\)