Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Ta có ![]()
![]()
Do đó số phức z có phần thực bằng 14 và phần ảo bằng 2 5

Đặt \(z=x+yi\Rightarrow w=\dfrac{1}{\sqrt{x^2+y^2}-x-yi}=\dfrac{\sqrt{x^2+y^2}-x+yi}{\left(\sqrt{x^2+y^2}-x\right)^2+y^2}\)
\(\Rightarrow\dfrac{\sqrt{x^2+y^2}-x}{\left(\sqrt{x^2+y^2}-x\right)^2+y^2}=\dfrac{1}{8}\Rightarrow\dfrac{\sqrt{x^2+y^2}-x}{2x^2+2y^2-2x\sqrt{x^2+y^2}}=\dfrac{1}{8}\)
\(\Rightarrow\dfrac{\sqrt{x^2+y^2}-x}{\sqrt{x^2+y^2}\left(\sqrt{x^2+y^2}-x\right)}=\dfrac{1}{4}\Rightarrow\dfrac{1}{\sqrt{x^2+y^2}}=\dfrac{1}{4}\)
\(\Rightarrow x^2+y^2=16\)
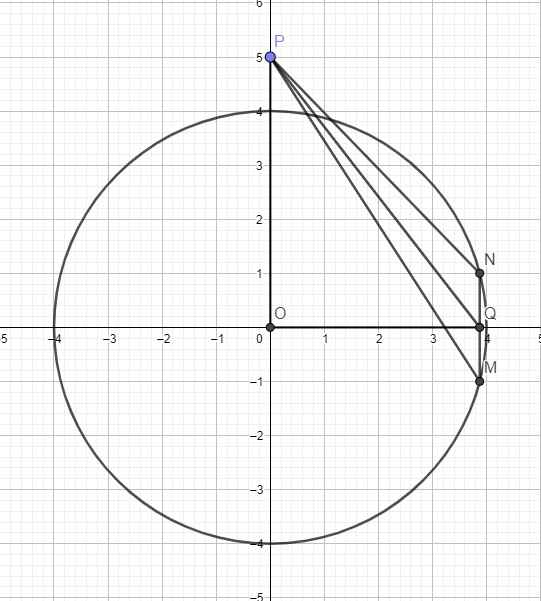
\(\Rightarrow\) Tập hợp \(z_1;z_2\) là đường tròn tâm O bán kính \(R=4\)
Gọi M, N lần lượt là điểm biểu diễn \(z_1;z_2\), do \(\left|z_1-z_2\right|=2\Rightarrow MN=2\)
Gọi \(P\left(0;5\right)\) và Q là trung điểm MN
\(\Rightarrow P=MP^2-NP^2=\overrightarrow{MP}^2-\overrightarrow{NP}^2=\left(\overrightarrow{MP}-\overrightarrow{NP}\right)\left(\overrightarrow{MP}+\overrightarrow{NP}\right)\)
\(=2\overrightarrow{MN}.\overrightarrow{PQ}=2\overrightarrow{MN}\left(\overrightarrow{PO}+\overrightarrow{OQ}\right)=2\overrightarrow{MN}.\overrightarrow{PO}=2MN.PO.cos\alpha\)
Trong đó \(\alpha\) là góc giữa \(MN;PO\)
Do MN, PO có độ dài cố định \(\Rightarrow P_{max}\) khi \(cos\alpha_{max}\Rightarrow\alpha=0^0\Rightarrow MN||PO\)
Mà MN=2 \(\Rightarrow M\left(\sqrt{15};-1\right);N\left(\sqrt{15};1\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{PM}=\left(\sqrt{15};-6\right)\\\overrightarrow{PN}=\left(\sqrt{15};-4\right)\end{matrix}\right.\)
\(\Rightarrow P_{max}=PM^2-PN^2=15+36-\left(15+16\right)=20\)

Đặt $z=a+bi$ ( $a,b\in\mathbb{R}$)
Theo bài ra ta có:
\(10(a+bi)+2i-3=(4-5i)(a+bi)+3i\Leftrightarrow (6a-5b-3)+i(6b-1+5a)=0\)
\(\Rightarrow \left\{\begin{matrix} 6a-5b-3=0\\ 5a+6b-1=0\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a=\frac{23}{61}\\ b=\frac{-9}{61}\end{matrix}\right.\). Do đó số \(z=\frac{23}{61}-\frac{9i}{61}\)
Vậy:
-Phần thực: $a=\frac{23}{61}$
-Phần ảo: $b=\frac{-9}{61}$
-Số phức liên hợp \(\overline{z}=a-bi=\frac{23}{61}+\frac{9i}{61}\)
-Mô đun: \(|z|=\sqrt{a^2+b^2}=\frac{\sqrt{610}}{61}\)

a) Đường phân giác của góc phần tư thứ nhất và góc pần tư thứ ba.
b) Đường phân giác của góc phần tư thứ hai và góc phần tư thứ tư.
c) Đường thẳng y = 2x + 1
d) Nửa đường tròn tâm O bán kính bằng 1, nằm bên phải trục Oy.


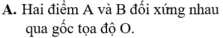
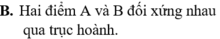
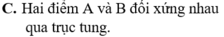
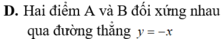

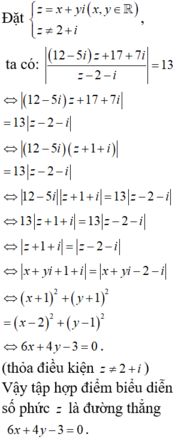
Đáp án D