K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
15 tháng 9 2023
a: A={0;1;4;...}
b: B={1;-1;2;-2;3;-3;4;-4;6;-6;12;-12}
c: C=B(120)={0;120;...}
H9
HT.Phong (9A5)
CTVHS
8 tháng 11 2023
Ta có số: 456** để số này chia hết cho 5 thì * bằng 5 hoặc 0
Với * = 5 thì số đó có dạng 45655 mà số này chia hết cho 4 do 55 không chia hết cho 4
Nên loại
Với * = 0 thì số đó có dạng 45600 có 0 ⋮ 4 nên 45600 ⋮ 4 thử lại thì 45600 ⋮ 6 thỏa mãn đề bài
13 tháng 9 2021
có góc ABC là góc tù vì 360-90-90-60=120
vậy CM \(\ge\)BC
vậy độ dài đoạn CM hay đọ dài vecto CM nhỏ nhất khi bằng BC
khi đó min(CM)=?
từ B hạ chân đường vuống góc xuống CD
khi đó ta dễ tính ra được BC=2a
từ C hà đường vuông góc tới AB
khi đó \(|\overrightarrow{CM}|^2\)=CM^2 = CH^2 + HM^2
vì CH không đổi nên ta không tính đến nó
có HM bé hơn hoặc bằng HA
vậy AC>= CM
vậy max(CM)=AC=\(2\sqrt{2}a\)
13 tháng 2 2023
a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-6}{2\cdot4}=\dfrac{-6}{8}=\dfrac{-3}{4}\\y=-\dfrac{6^2-4\cdot4\cdot\left(-5\right)}{4\cdot4}=-\dfrac{29}{4}\end{matrix}\right.\)
Bảng biến thiên là:
| x | -\(\infty\) -3/4 +\(\infty\) |
| y | -\(\infty\) -29/4 +\(\infty\) |
b: Hàm số đồng biến khi x>-3/4; nghịch biến khi x<-3/4
GTNN của hàm số là y=-29/4 khi x=-3/4
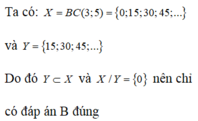
60 và 280
Ta có: 60 = 23 . 3 . 5
280 = 22 . 5 . 7
BCNN(60;280) = 23 . 3 . 5 . 7 = 840
84 và 108
Ta có: 84 = 22 . 3 . 7
108 = 22 . 33
BCNN(84;108) = 22 . 33 . 7 = 756
13 và 15
Vì 13 là số nguyên tố nên BCNN (13, 15) = 13 . 15 = 195.
60 và 280
ta có :
60=22.3.5
280=23.5.7
Vậy BCNN(60;280)=23.3.5.7=840.