Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

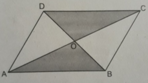
Xem hình bs.52.
- Các tam giác ADB, ACB, DAC, DBC có diện tích bằng nhau vì cùng bằng nửa diện tích hình bình hành đã cho.
- Các tam giác OAD, OCB, ODC, OBA có diện tích bằng nhau vì cùng bằng một phần tư diện tích hình bình hành đã cho.

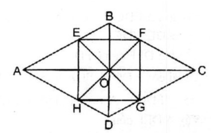
Ta có: ∠ (AOB) và ∠ (COD) đối đỉnh nên E, O, G thẳng hàng
∠ (BOC) và ∠ (AOD) đối đỉnh nên F, O, H thẳng hàng
Xét ∆ BEO và ∆ BFO:
∠ (EBO) = ∠ (FBO) (tính chất hình thoi)
OB cạnh chung
∠ (EOB) = ∠ (FOB) = 45 0 (gt)
Do đó: ∆ BEO = ∆ BFO (g.c.g)
⇒ OE = OF (1)
Xét ∆ BEO và ∆ DGO:
∠ (EBO) = ∠ (GDO) (so le trong)
OB = OD(tính chất hình thoi)
∠ (EOB) = ∠ (GOD) (đối đỉnh)
Do đó: ∆ BEO = ∆ DGO (g.c.g)
⇒ OE = OG (2)
Xét ∆ AEO và ∆ AHO:
∠ (EAO) = ∠ (HAO) (tính chất hình thoi)
OA cạnh chung
∠ (EOA) = ∠ (HOA) = 45 0 (gt)
Do đó: ∆ AEO = ∆ AHO (g.c.g)
⇒ OE = OH (3)
Từ (1), (2) và (3) suy ra: OE = OF = OG = OH hay EG = FH
nên tứ giác EFGH là hình chữ nhật (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường và bằng nhau)
OE ⊥ OF (tính chất tia phân giác của hai góc kề bù)
hay EG ⊥ FH
Vậy hình chữ nhật EFGH là hình vuông.

Ta có:
* SADB=SACB=SDAC=SDBC ( cùng bằng \(\dfrac{1}{2}.S_{hbh}\) )
* SOAD=SOCB=SODC=SOBA (cùng bằng \(\dfrac{1}{4}.S_{hbh}\))

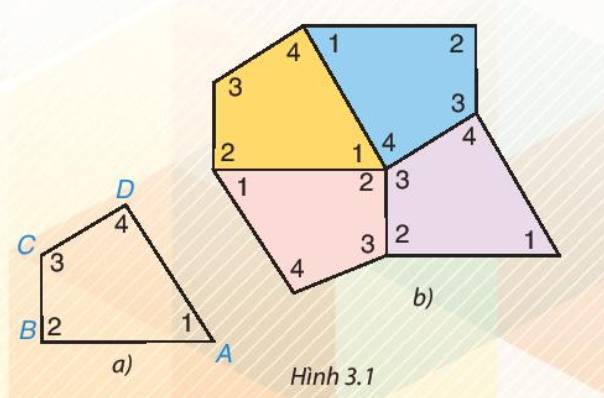
- Em cắt bốn tứ giác như nhau bằng giấy rồi thực hiện các bước theo yêu cầu bài toán.
Ta có thể ghép bốn tứ giác khít nhau như Hình 3.1b.
- Nhận xét: Bốn góc tại điểm chung của bốn tứ giác được ghép khít nhau.
Khi đó: \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)

Quá nhiều cách để chứng minh.
a. CE //BD
BE // DC ( vì DC // AB )
=> DCEB là hình bình hành
=> CE = BD
Mà BD =AC ( vì ABCD là hv)
=> CE = AC (1)
BD vuông AC ( vì ABCD là hình vuông )
mà CE // BD
=> CE vuông AC (2)
Từ (1); (2) => Tam giác ACE là tam giác vuông cân.
b) F đối xứng với AB qua O
=> AB là đường trung trực của OF
=> BF = BO và AO = AF
Mà OA = OB ( ABCD là hình bình hành vs O là giao 2 đường chéo )
=> BF = BO = AO = AF.
=> AOBF là hình thoi
Mặt khác ^AOB = 90^o
=> AOBF là hình vuông
c. APCQ là hình thoi
=>đường thẳng PQ là đường trung trực của đoạn AC (3)
Mặt khác ABCD là hình vuông => đường thẳng BD là đường trung trực của đoạn AC(4)
Từ (3); (4) => Đường thẳng PQ trùng đường thẳng BD => P; D; B; Q thẳng hàng.

+) Tam giác AOB và AOD có chung chiều cao hạ từ A xuống BD => S(AOB)/ S(AOD) = OB/OD
+) Tam giác COB và COD có chung chiều cao hạ từ C xuống BD => S(COB)/ S(COD) = OB/OD
=> S(AOB)/S(AOD) = S(COB)/ S(COD)
=> S(AOB). S(COD) = S(AOD).S(COB)
=> S(AOB).S(BOC).S(COD). (DOA) = [S(AOD).S(COB)]2 là số chính phương Vì S(AOD) và S(COB) nguyên
=> đpcm

Vì đường thẳng \(y = x\);\(y = x + 2\) song song với nhau và \(y = - x\);\(y = - x + 2\) song song với nhau nên tứ giác \(OABC\) là hình bình hành.
Lại có \(OC;OA\) là đường chéo của hình vuông có độ dài cạnh là 1 nên \(OC = OA\). Do đó, tứ giác \(OABC\) là hình thoi.
Lại có \(OC;OA\) là đường chéo của hình vuông nên cũng là đường phân giác. Do đó, \(\widehat {COB} = \widehat {AOB} = 45^\circ \Rightarrow \widehat {COA} = \widehat {COB} + \widehat {AOB} = 45^\circ + 45^\circ = 90^\circ \)
Hình thoi \(OABC\) có góc \(\widehat {COA} = 90^\circ \) nên tứ giác \(OABC\) là hình vuông.