x^2*(x-30)-31x+1

thay x=31 vao bieu thuc 

(31)^2*(31-30)-31*31+1=1

A= x^3(x-17) + 17x(x-1) +20

=16^3.(-1) +17.16.15+20 = (16+1)(16-1).16 -16^3+20

= (16^2-1).16 -16^3+20 = 16^3-16+16^3+20=4

B= x^4(x-15) + 16x^2(x-1) + 13x . (-x+1)

= -14^4 +16.14^2.13 + 13.14.(-13)= -14^4 +(15+1).14^2.13 -13^2.14

= -14^4 +15.14^2.13 + 14^2.13 - 13^2.14= -14^4 +(14+1).14^2.(14-1) -13^2.14

= -14^4 +(14^2-1).14^2 +13.14 = -14^4 +14^4 -14^2 +13.14= 14(13-14) = -14

\(A=x^4-17x^3+17x^2-17x+20\)

\(=x^4-\left(x+1\right)x^3+\left(x+1\right)x^2-\left(x+1\right)x+x+4\)

\(=x^4-x^4-x^3+x^3+x^2-x^2-x+x+4\)

\(=4\)

Ta đặt và thực hiện các phép tính P(x) + Q(x) và P(x) – Q(x).

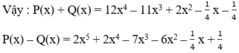
g(x) = x¹⁴ - 13x¹³ + 13x¹² - 13x¹¹ + ... + 13x² - 13x + 15

= x¹⁴ - (12 + 1)x¹³ + (12 + 1)x¹² - (12 + 1)x¹¹ + ... + (12 + 1)x² - (12 + 1)x + 15

Tại x = 12 thì ta có:

g(12) = x¹⁴ - (x + 1)x¹³ + (x + 1)x¹² - (x + 1)x¹¹ + ... + (x + 1)x² - (x + 1)x + 15

= x¹⁴ - x¹⁴ - x¹³ + x¹³ + x¹² - x¹² - x¹¹ + ... + x³ + x² - x² - x + 15

= -x + 15

Thay x = 12, ta có:

g(12) = -12 + 15 = 3

Vậy g(12) = 3

hơi khó hiểu nên có j thì cứ hỏi mik nhé!

a: \(=\dfrac{x^3-3x^2-7x+x^2-3x-7}{x^2-3x-7}=x+1\)

b:\(=\dfrac{x^3+x^2+3x^2+3x+5x+5}{x+1}=x^2+3x+5\)

c:\(=\dfrac{x^3-3x^2-7x+2x^2-6x-14}{x^2-3x-7}=x+2\)

d: \(=\dfrac{x^2\left(x+5\right)+5x+25-25}{x+5}=x^2+5-\dfrac{25}{x+5}\)

a: \(=\dfrac{3x^4-12x^3+12x^3-48x^2+47x^2-168x+168x-672+673}{x-4}\)

\(=3x^3+12x^2+47x+168+\dfrac{673}{x-4}\)

b: \(=\dfrac{x^4-3x^3-7x^2+3x^3-9x^2-21x+15x^2-45x-105+53x+91}{x^2-3x-7}\)

\(=x^2+3x+15+\dfrac{53x+91}{x^2-3x-7}\)

c: \(=\dfrac{x^3-3x^2-7x+x^2-3x-7}{x^2-3x-7}=x+1\)

\(f\left(x\right)=x^3-x+7\)

\(g\left(x\right)=-x^3+8x-14\)

\(\Rightarrow f\left(x\right)+g\left(x\right)=7x-7\)

Nghiệm của đa thức \(f\left(x\right)+g\left(x\right)=0\Rightarrow7x-7=0\)

\(\Rightarrow x=1\)

1)

`7x^2 -49x=0`

`<=>x(7x-49)=0`

\(< =>\left[{}\begin{matrix}x=0\\7x-49=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=0\\x=7\end{matrix}\right.\)

2)

`8x^2 -16x=0`

`<=>x(8x-16)=0`

\(< =>\left[{}\begin{matrix}x=0\\8x-16=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)

3)

`2x^3 +40x=0`

`<=>x(2x^2 +40)=0`

`<=>x=0` hoặc`2x^2 +40=0`

`<=>x=0` hoặc `2x^2 =-40` (vô lí vì `2x^2` luôn lớn hơn hoặc bằng 0)

`<=>x=0`

4)

`-x^3 +16x=0`

`<=>x^3 -16x=0`

`<=>x(x^2 -16)=0`

\(< =>\left[{}\begin{matrix}x=0\\x^2-16=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=0\\x^2=16\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\)