
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


(14,78-a)/(2,87+a)=4/1
14,78+2,87=17,65
Tổng số phần bằng nhau là 4+1=5
Mỗi phần có giá trị bằng 17,65/5=3,53
=>2,87+a=3,53
=>a=0,66.
a) A= 54 . 34- (152-1).(152+1)
=(5.3)4-154-1
=154-154-1
=-1

a) Ta có 15.64 + 25.100 + 36.15 + 60.100
= (15.64 + 36.15) + (25.100 + 60.100)
= 100.(15 + 85) = 10000.
b) Ta có 47 2 + 48 2 - 25 + 94.48
= ( 47 2 +2.47.48+ 48 2 ) - 5 2 = ( 47 + 48 ) 2 - 5 2 =9000.
c) Ta có 93 -92.(-l)-9.11 + (-l).ll
= (93 +92)-(9.11 + 1.11)
= 92(9 +1) -ll.(9 + l) = 700.

\(a,=15\left(64+36\right)+100\cdot25+100\cdot60\\ =100\left(15+25+60\right)=100\cdot100=10000\\ b,Sửa:47^2+48^2-25^2+94\cdot48=\left(47+48\right)^2-25^2\\ =95^2-25^2=\left(95-25\right)\left(95+25\right)=70\cdot120=8400\)

1.
$=153^2+2.47.153+47^2=(153+47)^2=200^2=40000$
2.
$=1,24^2-2.1,24.0,24+0,24^2=(1,24-0,24)^2=1^2=1$
3. Không phù hợp để tính nhanh
4.
$=15^8-(15^8-1)=1$
5.
$=(1^2-2^2)+(3^2-4^2)+(5^2-6^2)+...+(2019^2-2020^2)$
$=(1-2)(1+2)+(3-4)(3+4)+(5-6)(5+6)+...+(2019-2020)(2019+2020)$
$=(-1)(1+2)+(-1)(3+4)+(-1)(5+6)+....+(-1)(2019+2020)$
$=(-1)(1+2+3+4+....+2019+2020)=(-1).2020(2020+1):2=-2041210$
6:
\(\left(2+1\right)\left(2^2+1\right)\left(2^4+1\right)....\left(2^{2020}+1\right)+1\\ =1.\left(2+1\right)\left(2^2+1\right)\left(2^4+1\right)....\left(2^{2020}+1\right)+1\\ =\left(2-1\right)\left(2+1\right)\left(2^2+1\right)\left(2^4+1\right)....\left(2^{2020}+1\right)+1\\ =\left(2^2-1\right)\left(2^2+1\right)\left(2^4+1\right)....\left(2^{2020}+1\right)+1\\ =\left(2^4-1\right)\left(2^4+1\right)....\left(2^{2020}+1\right)+1\\ =\left(2^8-1\right)....\left(2^{2020}+1\right)+1\\ =\left(2^{2020}-1\right)\left(2^{2020}+1\right)+1\\ =2^{4040}-1+1=2^{4040}\)

Lời giải:
Đặt $A=x^{2011}+x^{2010}+....+x+1$
$Ax=x^{2012}+x^{2011}+...+x^2+x$
$\Rightarrow Ax-A=x^{2012}-1$
$\Rightarrow A=\frac{x^{2012}-1}{x-1}$
$B=x^{502}+x^{501}+...+x+1$
$Bx=x^{503}+x^{502}+....+x^2+x$
$\Rightarrow Bx-B=x^{503}-1$
$\Rightarrow B=\frac{x^{503}-1}{x-1}$
Khi đó: $A:B = \frac{x^{2012}-1}{x-1}: \frac{x^{503}-1}{x-1}=\frac{x^{2012}-1}{x^{503}-1}=\frac{(x^{503})^4-1}{x^{503}-1}$
Đặt $x^{503}=a$ thì:
$A:B=\frac{a^4-1}{a-1}=a^3+a^2+a+1$
$\Rightarrow A\vdots B$

SSH:(20152-12):10+1=2015
(12-22)+(32-42)+(52-62)+...+(20132-20142)+20152
-10+(-10)+(-10)+...+(-10)+20152
-10x(2015-1):2+20152=12
=> C=12

a) \(=\left(127+73\right)^2=200^2=40000\)
b) \(=18^8-\left(18^8-1\right)=1\)
c) \(=\left(100+99\right)\left(100-99\right)+\left(98+97\right)\left(98-97\right)+...+\left(2+1\right)\left(2-1\right)\)
\(=100+99+98+97+...+2+1=5050\)
d) biến đổi thành \(20^2-19^2+18^2-17^2+..+2^2-1^2\)
rồi giải ra như trên
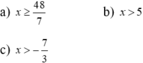
bạn nào trả lời cho mình đi