
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Như lời ở câu hỏi trước, mình làm ý (b) ở đây nha=)
Áp dụng định lý cosin cho các góc A, B và C, ta có:
`a^2 = b^2 + c^2 - 2bc.cosA`
`b^2 = a^2 + c^2 - 2ac.cosB`
`c^2 = a^2 + b^2 - 2abcosC`
Thay các công thức trên vào biểu thức cần chứng minh, ta có:
`sin^2A + sin^2B + sin^2C = (a^2/c^2) + (b^2/c^2) + (c^2/c^2)`
`= (a^2 + b^2 + c^2)/(c^2)`
`= (a^2 + b^2 + c^2)/(a^2 + b^2 - 2abcosC)`
`= [(a^2 + b^2 + c^2) + 2abcosC]/(a^2 + b^2 - 2abcosC)`
`= [2(a^2 + b^2 - abcosC)]/(a^2 + b^2 - 2abcosC)`
`= 2(1 + cosAcosBcosC)`


12.
\(y=\sqrt{2}sin\left(2x+\dfrac{\pi}{4}\right)\le\sqrt[]{2}\)
\(\Rightarrow M=\sqrt{2}\)
13.
Pt có nghiệm khi:
\(5^2+m^2\ge\left(m+1\right)^2\)
\(\Leftrightarrow2m\le24\)
\(\Rightarrow m\le12\)
14.
\(\Leftrightarrow\left[{}\begin{matrix}cosx=1\\cosx=-\dfrac{5}{3}\left(loại\right)\end{matrix}\right.\)
\(\Leftrightarrow x=k2\pi\)
15.
\(\Leftrightarrow\left[{}\begin{matrix}tanx=-1\\tanx=3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=arctan\left(3\right)+k\pi\end{matrix}\right.\)
Đáp án A
16.
\(\dfrac{\sqrt{3}}{2}sinx-\dfrac{1}{2}cosx=\dfrac{1}{2}\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{6}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{6}=\dfrac{\pi}{6}+k2\pi\\x-\dfrac{\pi}{6}=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=\pi+k2\pi\end{matrix}\right.\)
\(\left[{}\begin{matrix}2\pi\le\dfrac{\pi}{3}+k2\pi\le2018\pi\\2\pi\le\pi+k2\pi\le2018\pi\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}1\le k\le1008\\1\le k\le1008\end{matrix}\right.\)
Có \(1008+1008=2016\) nghiệm



1.
\(sin^2x-4sinx.cosx+3cos^2x=0\)
\(\Rightarrow\dfrac{sin^2x}{cos^2x}-\dfrac{4sinx}{cosx}+\dfrac{3cos^2x}{cos^2x}=0\)
\(\Rightarrow tan^2x-4tanx+3=0\)
2.
\(\Leftrightarrow\dfrac{1}{2}cos2x+\dfrac{\sqrt{3}}{2}sin2x=\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(2x-\dfrac{\pi}{3}\right)=\dfrac{1}{2}\)
3.
\(\Leftrightarrow2^2+m^2\ge1\)
\(\Leftrightarrow m^2\ge-3\) (luôn đúng)
Pt có nghiệm với mọi m (đề bài sai)
4.
\(\Leftrightarrow\dfrac{1}{2}sinx-\dfrac{\sqrt{3}}{2}cosx=1\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{3}\right)=1\)
\(\Leftrightarrow x-\dfrac{\pi}{3}=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=\dfrac{5\pi}{6}+k2\pi\)
6.
ĐKXĐ: \(cosx\ne0\)
Nhân 2 vế với \(cos^2x\)
\(sin^2x-4cosx+5cos^2x=0\)
\(\Leftrightarrow1-cos^2x-4cosx+5cos^2x=0\)
\(\Leftrightarrow\left(2cosx-1\right)^2=0\)
\(\Leftrightarrow cosx=\dfrac{1}{2}\Rightarrow x=\pm\dfrac{\pi}{3}+k2\pi\)

6.
\(cos^2x+\sqrt{3}sinx.cosx-1=0\)
\(\Leftrightarrow-sin^2x+\sqrt{3}sinx.cosx=0\)
\(\Leftrightarrow sinx\left(sinx-\sqrt{3}cosx\right)=0\)
\(\Leftrightarrow sinx\left(\dfrac{1}{2}sinx-\dfrac{\sqrt{3}}{2}cosx\right)=0\)
\(\Leftrightarrow sinx.sin\left(x-\dfrac{\pi}{3}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\sin\left(x-\dfrac{\pi}{3}\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\dfrac{\pi}{3}+k\pi\end{matrix}\right.\)

1.
\(\Leftrightarrow1+2sin\dfrac{x}{2}cos\dfrac{x}{2}+\sqrt{3}cosx=3\)
\(\Leftrightarrow sinx+\sqrt{3}cosx=2\)
\(\Leftrightarrow\dfrac{1}{2}sinx+\dfrac{\sqrt{3}}{2}cosx=1\)
\(\Leftrightarrow cos\left(x-\dfrac{\pi}{6}\right)=1\)
\(\Leftrightarrow x-\dfrac{\pi}{6}=k2\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+k2\pi\)
2.
\(cos2x=-1\)
\(\Leftrightarrow2x=\pi+k2\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{2}+k\pi\)
3.
\(\left(2sinx-cosx\right)\left(1+cosx\right)=\left(1+cosx\right)\left(1-cosx\right)\)
\(\Leftrightarrow\left(1+cosx\right)\left(2sinx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=-1\\sinx=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\pi+k2\pi\\x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
Nghiệm dương nhỏ nhất là \(x=\dfrac{\pi}{6}\)
4.
\(1-cos2x-1-cos6x=0\)
\(\Leftrightarrow cos6x=-cos2x=cos\left(\pi-2x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}6x=\pi-2x+k2\pi\\6x=2x-\pi+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{8}+\dfrac{k\pi}{4}\\x=-\dfrac{\pi}{4}+\dfrac{k\pi}{2}\end{matrix}\right.\)
Pt có 6 nghiệm trên khoảng đã cho
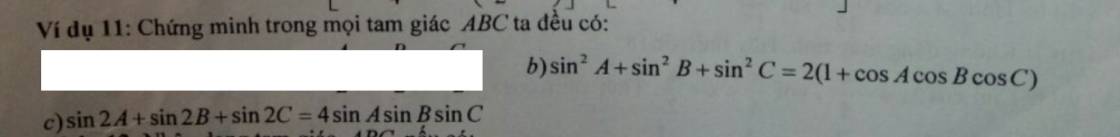
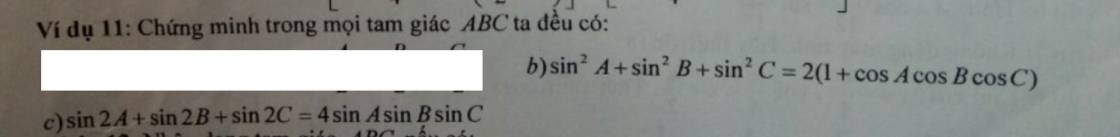









b)
Trong tam giác ABC có:
`sin^2(A) = 1 - cos^2(A) = 1 - (2sin(A/2)cos(A/2))^2 = 1 - 4sin^2(A/2)cos^2(A/2) = 1 - 4sin^2(A/2)(1 - sin^2(A/2)) = 4sin^2(A/2)sin^2(B/2)sin^2(C/2)`
Với R là bán kính đường tròn ngoại tiếp tam giác ABC và r là bán kính đường tròn nội tiếp tam giác ABC:
`sin^2(A) = 4sin^2(A/2)sin^2(B/2)sin^2(C/2) = 4(1/8R/r)^2 = 1/2^2R^2/r^2 = 1/4R^2/r^2`
Với a, b, c là độ dài các cạnh tam giác ABC và S là diện tích tam giác ABC:
`sin^2(A) = 1/4R^2/r^2 = 1/4(abc / 4S)^2/r^2 = abc^2 / 16S^2r^2`
Với r là bán kính đường tròn nội tiếp tam giác ABC:
`sin^2(A) = abc^2 / 16S^2r^2 = abc^2 / 16[(a + b + c)r / 2]^2r^2 = abc^2 / 16(a + b + c)^2r^3`
Áp dụng tương tự với `sin^2B` và `sin^2C`
Tổng các biểu thức trên:
`sin^2(A) + sin^2(B) + sin^2(C) = abc^2 / 16(a + b + c)^2r^3 + bca^2 / 16(b + c + a)^2r^3 + cab^2 / 16(c + a + b)^2r^3
= (abc^2 + bca^2 + cab^2) / 16(a + b + c)^2r^3
= 4sin(A)sin(B)sin(C)`
Bạn chứng minh cách khác được không ạ