Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

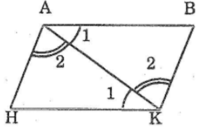
Nối AK, ta có:
AB // HK (giả thiết)
⇒ ∠(A1 ) =∠(K1 ) (hai góc so le trong)
+) Lại có: AH // BK (giả thiết)
⇒ ∠ (A2 ) = ∠(K2 ) (hai góc so le trong)
Xét ΔABK và ΔKHA, ta có:
∠(A1 ) =∠(K1 ) ( chứng minh trên)
AK cạnh chung
∠(K2 ) =∠(A2 ) (chứng minh trên)
Suy ra: ΔABK =ΔKHA (g.c.g)
Vậy: AB = KH; BK = AH ( 2 cạnh tương ứng)

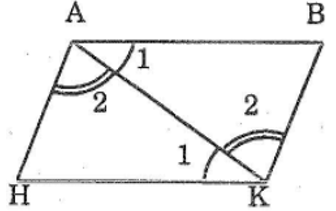
Nối A với K
Xét tam giác ABK và tam giác AHK có:
AK: cạnh chung
góc BAK = góc AKH (AB // HK)
góc HAK = góc AKB (AH //BK)
=> tam giác ABK = tam giác AHK
=> AB = HK (hai cạnh tương ứng)
Ta có: tam giác ABK = tam giác AHK
=> AH = BK (hai cạnh tương ứng)
kẻ đoạn thẳng AK
Xét tamgiác KAH và tam giác AKB
góc HAK = góc BKA (2 góc so le trong do AK cắt AH// BK )
cạnh AK chung
góc HKA = góc BAK (2 góc so le trong do AB //HK )
=> tam giác KAH = tam giác AKB ( g.c.g.)
=> AB=HK (2 cạnh tương ướng )
=> AH = BK (2 cạnh tương ướng )
đúng không..............................................

Bn tự vẽ hình nha
Xét tg AHB và tg AHC có
AB=AC; góc AHB = góc AHC =90 độ;
Ah cạnh chung
=> tg AHB = tg AHC (ch cgv)
=> BH = HC
=> H là trung điểm BC
Xét tg BKC có
H là trung điểm BC (cmt)
DH//KC ( gt)
=> D là trung điểm BK
( đpcm )
Ầy mk chỉ biết câu a thui mà đằng nào chúng ta mới 2k5 thui biết vận dụng cả lớp 8 là tốt lắm rùi ....!

đề bạn thiếu là Cho tam giác ABC vuông tại A
A) VÌ Hx// AD HAY Hx // AC
=> \(\widehat{H_1}+\widehat{A_1}=180^o\)( trong cùng phía )
mà \(\widehat{H_1}=90^o\)
\(\Rightarrow\widehat{A_1}=90^o\)
mà Dy // AH HAY DK // BH
\(\Rightarrow\widehat{D_1}=\widehat{A_2}=90^o\)(SO LE TRONG)
VÌ Hx // AC
\(\Rightarrow\widehat{K_1}+\widehat{D_1}=180^o\)(trong cùng phía)
MÀ \(\widehat{D_1}=90^o\)
\(\Rightarrow\widehat{K_1}=90^o\)
XÉT TỨ GIÁC \(HADK\)CÓ
\(\widehat{K_1}=\widehat{D_1}=\widehat{A_1}=\widehat{H_1}=90^o\)
VÀ HAI CẠNH HA = AD
=> TỨ GIÁC \(HADK\)LÀ HÌNH VUÔNG
=> \(AH=HK=DK\)(ĐPCM)
B) TA CÓ \(AC=3AB\)
MÀ \(AB=AD\)
=>\(AC=3AD\)
NÊN \(DC=2AD\left(1\right)\)
TA CÓ \(AD=AH=AB\left(GT\right)\)
=> \(2AD=AH+AB\)
=>\(2AD=HB\left(2\right)\)
THAY (2) VÀO (1)
\(\Rightarrow DC=HB\)
XÉT \(\Delta BHK\)VÀ \(\Delta CDK\)CÓ
\(HK=DK\left(CMT\right)\)
\(\widehat{H_1}=\widehat{D_2}=90^o\)
\(BH=CD\left(CMT\right)\)
=>\(\Delta BHK\)=\(\Delta CDK\)(C-G-C)
\(\Rightarrow BK=KC\)(ĐPCM)
=> \(\widehat{K_4}=\widehat{K_3}\)
MÀ \(\widehat{HKD}=90^o\)
=> \(\widehat{K_4}+\widehat{K_2}=90^o\)
mà \(\widehat{K_4}=\widehat{K_3}\)
=>\(\widehat{K_3}+\widehat{K_2}=90^o\)
=>\(\widehat{BKC}=90^o\)
=>\(BK\perp KC\left(ĐPCM\right)\)
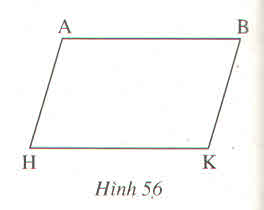
Mình không thể vẽ ra hình đề bài cho được.