
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a. Phương trình hoành độ giao điểm:
\(3x-5=-2x\)
\(\Leftrightarrow5x=5\)
\(\Rightarrow x=1\)
Thế vào \(y=3x-5\Rightarrow y=3.1-5=-2\)
Vậy \(A\left(1;-2\right)\)
b. Gọi phương trình d có dạng \(y=ax+b\)
Do d song song \(d_1\Rightarrow a=1\Rightarrow y=x+b\)
Do d qua A nên: \(y_A=x_A+b\Leftrightarrow-2=1+b\Rightarrow b=-3\)
Vậy pt d có dạng: \(y=x-3\)

ta có sinB=\(\dfrac{AH}{AB}\)\(\Rightarrow\)AH=AB.sinB=3,6.sin62=3,18
BH=\(\sqrt{AB^2-AH^2}\)(pytago)=\(\sqrt{3,6^2-3,18^2}\)=1,69
\(_{\widehat{C}}\)=90-\(\widehat{B}\)=90-62=28\(^0\)
sinC=\(\dfrac{AB}{BC}\)\(\Rightarrow\)BC=\(\dfrac{AB}{sinC}\)=\(\dfrac{3,6}{sin28}\)=7,67
mà:CH=BC-BH=7,67-1,69=5,98
AC=\(\sqrt{BC^2-AB^2}\)(pytago)=\(\sqrt{7,67^2-3,6^2}\)=6.77

Bài 2:
a) ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\notin\left\{4;9\right\}\end{matrix}\right.\)
b) Ta có: \(B=\dfrac{2\sqrt{x}-9}{x-5\sqrt{x}+6}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}-\dfrac{2\sqrt{x}+1}{3-\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}-9-\left(x-9\right)+\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{2\sqrt{x}-9-x+9+2x-4\sqrt{x}+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\cdot\left(\sqrt{x}-3\right)}\)
\(=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
c) Để B>1 thì B-1>0
\(\Leftrightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}-3}-\dfrac{\sqrt{x}-3}{\sqrt{x}-3}>0\)
\(\Leftrightarrow\dfrac{4}{\sqrt{x}-3}>0\)
\(\Leftrightarrow\sqrt{x}>3\)
hay x>9
Bài 2:
d) Để B nguyên thì \(\sqrt{x}+1⋮\sqrt{x}-3\)
\(\Leftrightarrow4⋮\sqrt{x}-3\)
\(\Leftrightarrow\sqrt{x}-3\in\left\{-2;-1;1;2;4\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{1;2;4;5;7\right\}\)
hay \(x\in\left\{1;16;25;49\right\}\)

a, Ta có : \(A=\dfrac{1}{x+\sqrt{x}}+\dfrac{1}{\sqrt{x}+1}=\dfrac{1}{\sqrt{x}\left(\sqrt{x}+1\right)}+\dfrac{1}{\sqrt{x}+1}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}\left(1+\sqrt{x}\right)}=\dfrac{1}{\sqrt{x}}\)
\(\Rightarrow P=\dfrac{A}{B}=\dfrac{\dfrac{1}{\sqrt{x}}}{\dfrac{2}{\sqrt{x}+1}}=\dfrac{1}{\sqrt{x}}.\dfrac{\sqrt{x}+1}{2}=\dfrac{\sqrt{x}+1}{2\sqrt{x}}\)
b, Ta có : \(P=\dfrac{\sqrt{x}+1}{2\sqrt{x}}=\dfrac{1}{2}+\dfrac{1}{2\sqrt{x}}\)
Mà \(x>0\)
\(\Rightarrow\dfrac{1}{2\sqrt{x}}>0\)
\(\Rightarrow P>\dfrac{1}{2}\)
Vậy ...

\(\begin{cases}\dfrac{1}{x+3}-\dfrac{2}{y-1}=9\\\dfrac{3}{x+3}+\dfrac{1}{y-1}=6\\\end{cases}\)
`<=>` \(\begin{cases}\dfrac{1}{x+3}-\dfrac{2}{y-1}=9\\\dfrac{6}{x+3}+\dfrac{2}{y-1}=12\\\end{cases}\)
`<=>` \(\begin{cases}\dfrac{7}{x+3}=21\\\dfrac{3}{x+3}+\dfrac{1}{y-1}=6\\\end{cases}\)
`<=>` \(\begin{cases}\dfrac{1}{x+3}=3\\\dfrac{3}{x+3}+\dfrac{1}{y-1}=6\\\end{cases}\)
`<=>` \(\begin{cases}x+3=\dfrac13\\\dfrac{1}{y-1}=6-9=-3\\\end{cases}\)
`<=>` \(\begin{cases}x=\dfrac{-8}{3}\\y=\dfrac23\\\end{cases}\)
ĐKXĐ : \(\left\{{}\begin{matrix}x\ne-3\\y\ne1\end{matrix}\right.\)
- Đặt \(\left\{{}\begin{matrix}\dfrac{1}{x+3}=a\\\dfrac{1}{y-1}=b\end{matrix}\right.\)
HPTTT : \(\left\{{}\begin{matrix}a-2b=9\\3a+b=6\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a-2b=9\\6a+2b=12\end{matrix}\right.\)
- Cộng hai phương trình ta được : 7a = 21
=> a = 3
=> b = -3
- Thay lại hệ phương trình ta được ; \(\left\{{}\begin{matrix}\dfrac{1}{x+3}=3\\\dfrac{1}{y-1}=-3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{8}{3}\\y=\dfrac{2}{3}\end{matrix}\right.\) ( TM )
Vậy ..
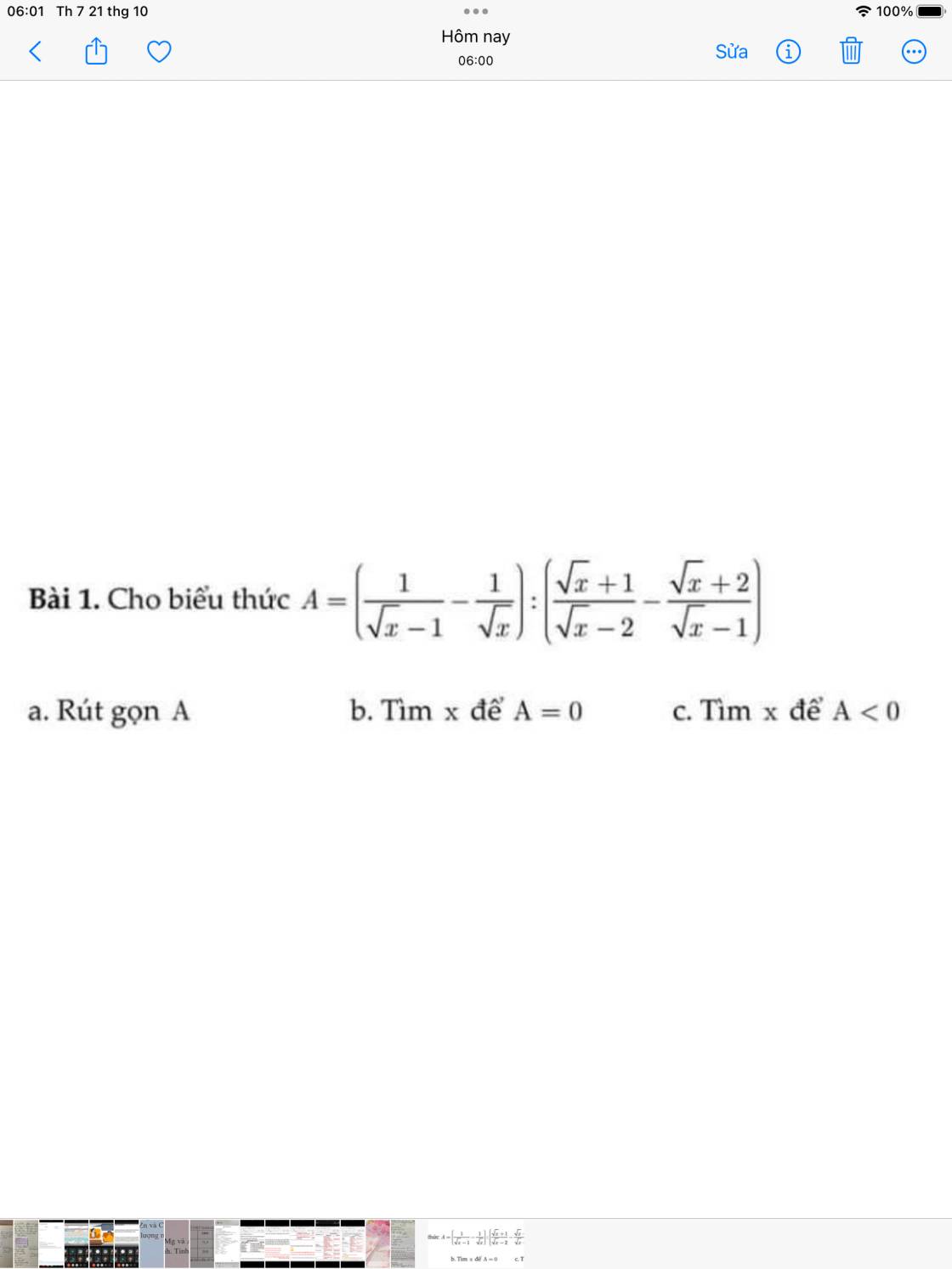





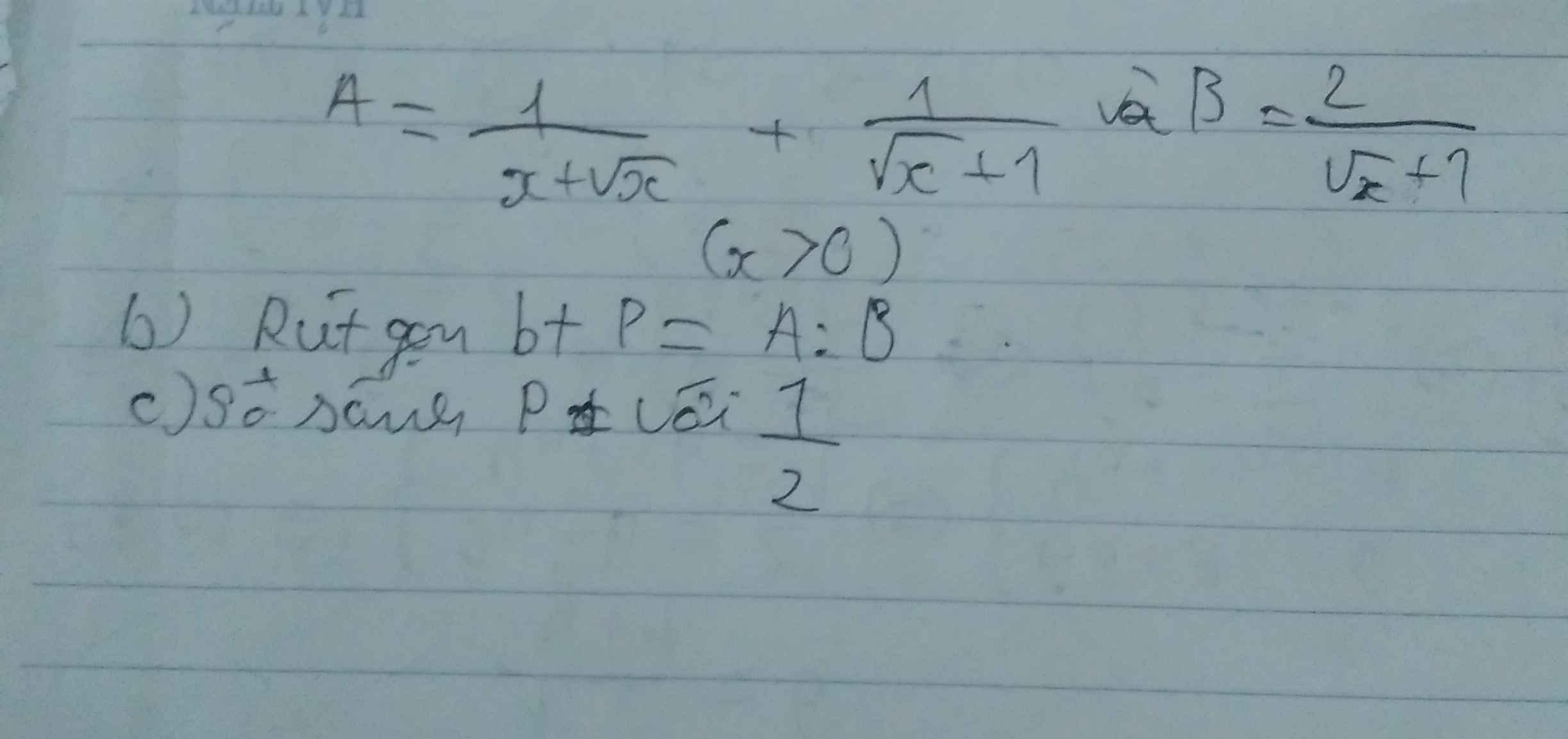

a. \(A=\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}}\right):\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-\dfrac{\sqrt{x}+2}{\sqrt{x}-1}\right)\) (ĐKXĐ: \(x>0;x\ne1;x\ne4\))
\(=\left[\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right]:\left[\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}-\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}\right]\)
\(=\dfrac{\sqrt{x}-\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{x-1-\left(x-4\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{x-1-x+4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}{3}\)
\(=\dfrac{\sqrt{x}-2}{3\sqrt{x}}\)
Vậy \(A=\dfrac{\sqrt{x}-2}{3\sqrt{x}}\).
\(---\)
b. Ta có: \(A=0\Leftrightarrow\dfrac{\sqrt{x}-2}{3\sqrt{x}}=0\)
\(\Leftrightarrow\sqrt{x}-2=0\)
\(\Leftrightarrow\sqrt{x}=2\)
\(\Leftrightarrow x=4\left(ktm\right)\)
Vậy không thể tìm được giá trị nào của \(x\) để \(A=0\).
\(---\)
c. Ta có: \(A< 0\Leftrightarrow\dfrac{\sqrt{x}-2}{3\sqrt{x}}< 0\)
\(\Leftrightarrow\sqrt{x}-2< 0\left(vì.3\sqrt{x}>0\right)\)
\(\Leftrightarrow\sqrt{x}< 2\)
\(\Leftrightarrow x< 4\)
Kết hợp với điều kiện xác định của \(x\), ta được:
\(0< x< 4;x\ne1\)
Vậy \(A< 0\) khi \(0< x< 4;x\ne1\).
a) \(A=\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}}\right):\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-\dfrac{\sqrt{x}+2}{\sqrt{x}-1}\right)\) (ĐK: \(x>0;x\ne1;x\ne4\))
\(A=\left[\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right]:\left[\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}-\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\right]\)
\(A=\dfrac{\sqrt{x}-\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{x-1-x+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\)
\(A=\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}{3}\)
\(A=\dfrac{\sqrt{x}-2}{3\sqrt{x}}\)
b) \(A=0\) khi
\(\dfrac{\sqrt{x}-2}{3\sqrt{x}}=0\)
\(\Rightarrow\sqrt{x}-2=0\)
\(\Rightarrow\sqrt{x}=2\)
\(\Rightarrow x=4\left(ktm\right)\)
c) \(A< 0\) khi
\(\dfrac{\sqrt{x}-2}{3\sqrt{x}}< 0\)
\(\Rightarrow\sqrt{x}-2< 0\)
\(\Rightarrow\sqrt{x}< 2\)
\(\Rightarrow x< 4\)
kết hợp với đk:
\(0< x< 4,x\ne1\)